题目

题目来源：力扣（LeetCode）

设计并实现一个算法，找出二叉树中某两个节点的第一个共同祖先。不得将其他的节点存储在另外的数据结构中。注意：这不一定是二叉搜索树。
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

  1. 3<br />   / \<br />  5   1<br /> / \ / \<br />6  2 0  8<br />  / \<br /> 7   4<br />示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

思路分析

p 、q 在二叉树中有以下三种情况：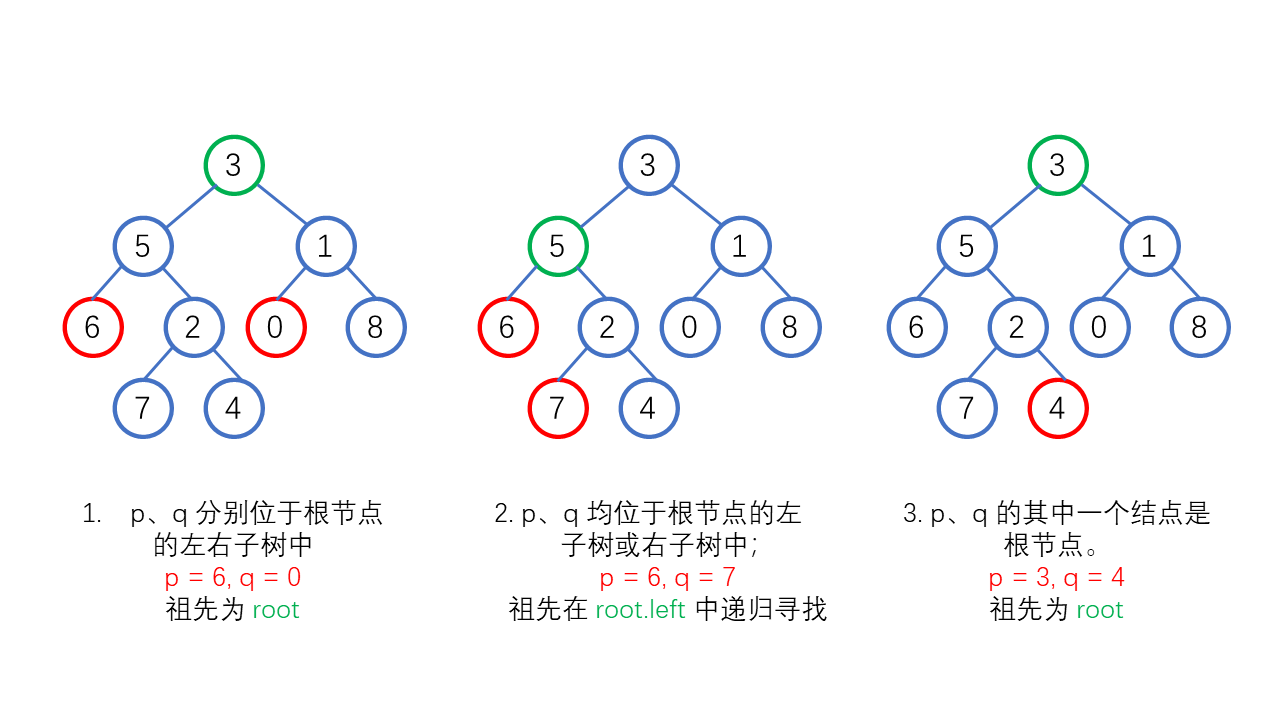
image.png

  • 我们从根节点开始，采用深度优先搜索算法(DFS) 向下遍历，如果当前节点到达叶子节点下的空节点时，返回 null；如果当前节点为 p 或 q ，则为情况3，我们返回当前的节点。

  • 我们继续在左子树中查找 p 或 q ，如果在左子树中找到了 p 或 q ，说明 p 或 q 在左子树中，将查找结果存储在变量 left 中。

  • 然后在右子树中查找 p 或 q ，如果找到了 ，说明 p 或 q 在右子树中，将查找结构存储在变量 right 中。

  • 然后我们进行判断：如果 left 和 right 都不为空，则为情况 1；如果 left 和 right 中只有一个不为空，说明这两个结点在子树中，则根节点到达子树再进行寻找。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val) {
  4.  *     this.val = val;
  5.  *     this.left = this.right = null;
  6.  * }
  7.  */
  8. /**
  9.  * @param {TreeNode} root
  10.  * @param {TreeNode} p
  11.  * @param {TreeNode} q
  12.  * @return {TreeNode}
  13.  */
  14. var lowestCommonAncestor = function(root, p, q) {
  15.   // 到底了，没有找到，返回 null
  16.   if (root == null) return null;
  17.   // p、q 的其中一个节点就是根节点，那么祖先就是p或q(谁是根节点，谁就是共同祖先)
  18.   if (root == p || root == q) return root;
  20.   let left = lowestCommonAncestor(root.left, p, q); // 在左子树中找到了 p 或 q
  21.   let right = lowestCommonAncestor(root.right, p, q); // 在右子树中找到了 p 或 q
  22.   // 如果 left 和 right 都不为空，说明这两个节点一个在当前节点的左子树上，一个在当前节点的右子树上
  23.   // 那么当前节点就是它们的共同祖先
  24.   if (left != null && right != null) return root;
  25.   // 如果 left 不为空，说明这两个节点都在当前节点的左子树上，返回左子树查找的结果
  26.   if (left != null) return left;
  27.   // 两个节点都在当前节点的右子树上，返回右子树查找的结果
  28.   if(right != null) return right;
  29. };