题目

题目来源：力扣（LeetCode）

给你一棵二叉树的根节点 root ，请你返回层数最深的叶子节点的和 。

示例 1：

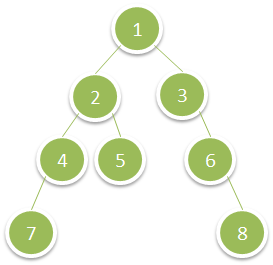
image.png

输入：root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
输出：15

示例 2：

输入：root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出：19

解法一：深度优先搜索

我们从根节点开始进行搜索，在搜索的同时记录当前节点的深度 depth 。定义两个全局变量 maxDepth 和 sum , 其中 maxDepth 表示搜索到的节点的最大深度，sum 表示搜索到的最大深度的节点的权值之和。

当我们搜索到一个新的节点 x 时，会有以下三种情况：

  • 节点 x 的深度 depth 小于 最大深度 maxDepth，那么我们可以忽略节点 x ，继续进行搜索；
  • 节点 x 的深度 depth 等于 最大深度 maxDepth，那么我们将节点 x 的权值添加到 sum 中；
  • 节点 x 的深度 depth 大于 最大深度 maxDepth，此时我们找到了一个深度更大的节点，因此需要将 maxDepth 置为当前找到的深度 depth ，并将 sum 的值置为节点 x 的权值。

在深度优先搜索结束之后，深度最大的叶子节点的权值之和就存储在 sum 中。

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number}
  4.  */
  5. var deepestLeavesSum = function (root) {
  6.   let sum = [0], maxDepth = [-1];
  7.   dfs(root, sum, 0, maxDepth);
  8.   return sum[0];
  9. };
  10. const dfs = (root, sum, depth, maxDepth) => {
  11.   if (root == null) {
  12.     return;
  13.   }
  14.   if (depth > maxDepth[0]) {
  15.     // 当前节点的深度 depth 大于 maxDepth，将 maxDepth 置为 depth，并将 sum 的值置为当前节点的权值
  16.     maxDepth[0] = depth;
  17.     sum[0] = root.val;
  18.   } else if (maxDepth[0] == depth) {
  19.     // 当前节点的深度等于 maxDepth，将节点的权值添加到 sum 中
  20.     sum[0] += root.val;
  22.   }
  23.   // 搜索左子树
  24.   dfs(root.left, sum, depth + 1, maxDepth);
  25.   // 搜索右子树
  26.   dfs(root.right, sum, depth + 1, maxDepth);
  27. }