三角形最小路径和

题目

题目来源：力扣（LeetCode）

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

思路分析

题目中，给定的三角形的行数为 n，并且第 i 行（从 0 开始编号）包含了 i + 1 个数。如果将每一行的左端对齐，那么会形成一个等腰直角三角形，如下所示：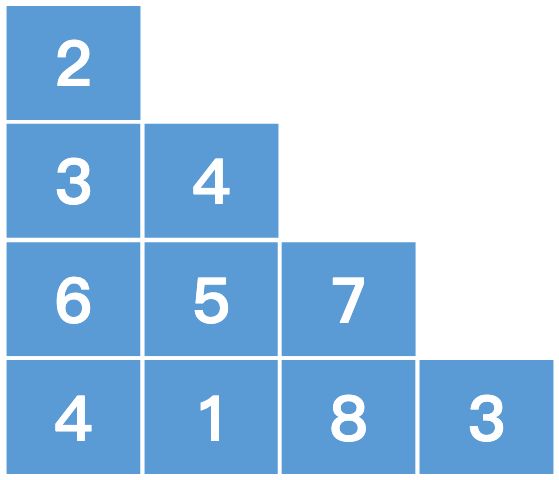

下图演示的是自下而上的推导过程：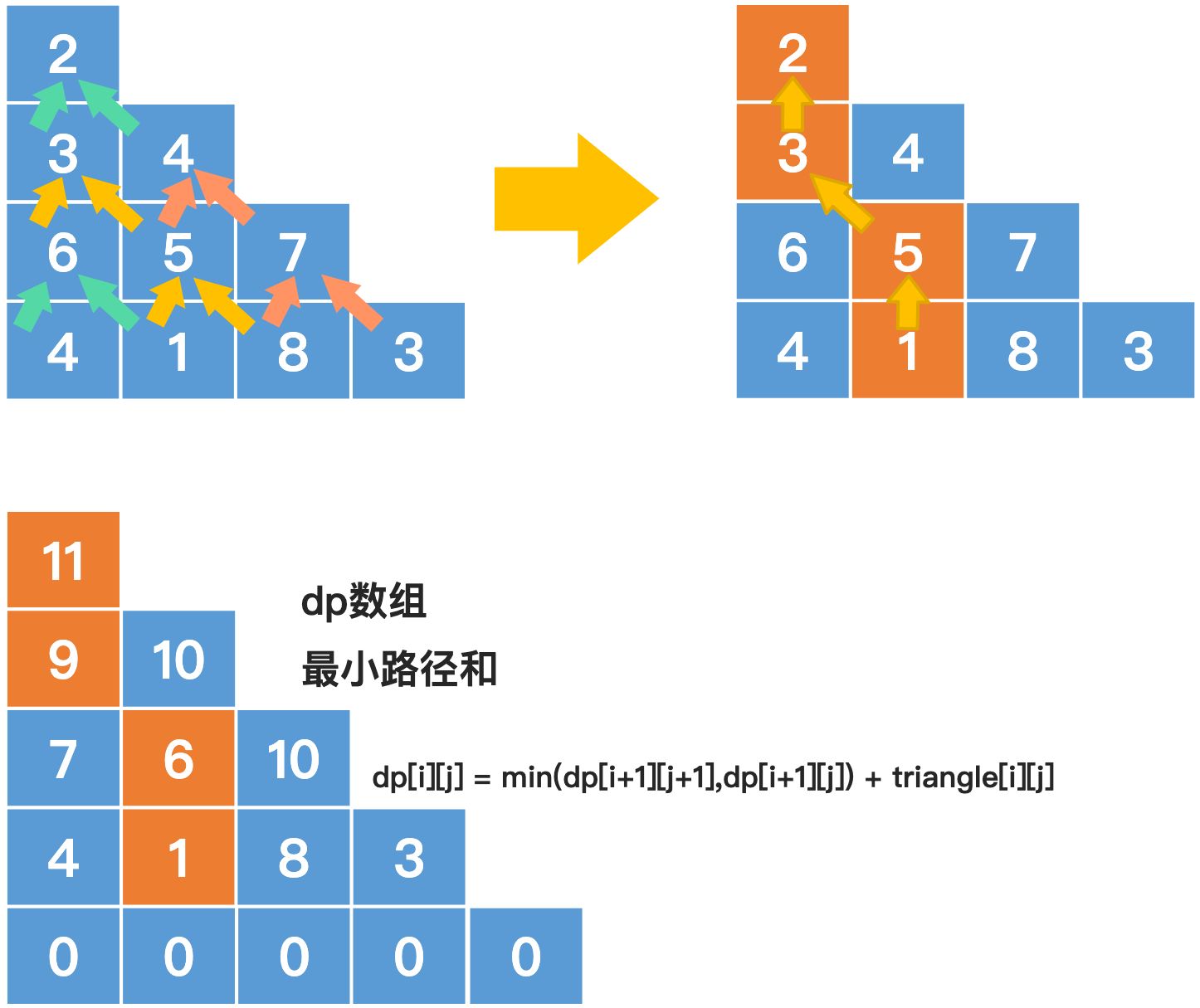

自下为上推导时，最终结果保存在第一行第一列中，，因为三角形第一行只有一个元素，所以最终结果就保存在 dp[0][0] 中。

这里的 dp数组是原始数组的行数 + 1，之所以要多加一行，是因为状态转移公式变化导致的，为了处理一些边界条件，所以增加了一行。

从自下而上的角度看，三角形中任意一个位置 trianglep[i][j] ，只有两个位置可以移动到 trianglep[i][j]，分别是： trianglep[i + 1][j + 1] 和 trianglep[i + 1][j]，如下图所示: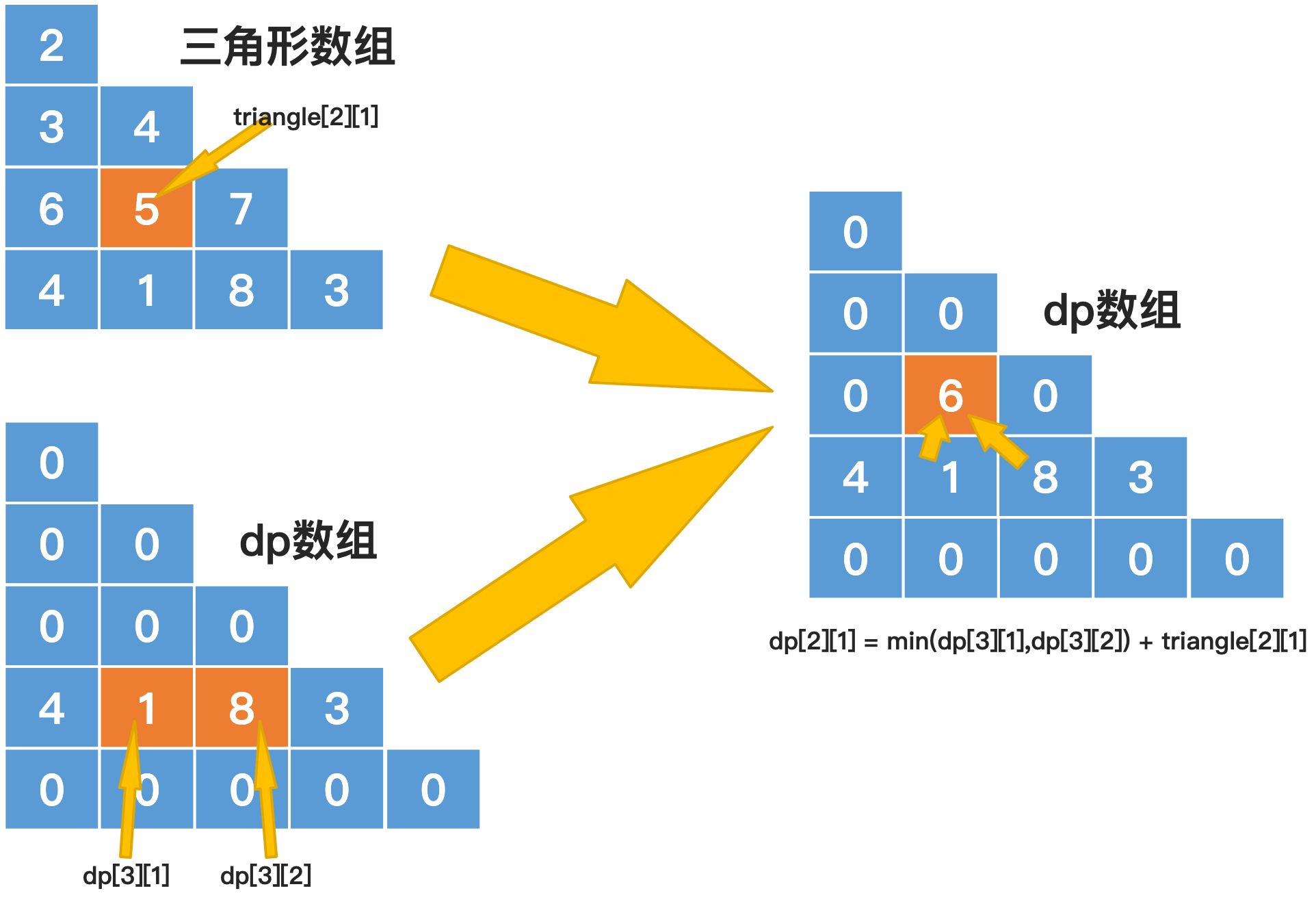

对于 triangle[2][1] 这个位置，它是从triangle[3][1]，以及triangle[3][2]这两个位置移动而来的。而这两个值保存在dp[3][1]和dp[3][2]中。

我们从dp[3][1]和dp[3][2]中选择一个较小的值，这里是1，然后再加上triangle[2][1]的值5，将结果6保存到dp[2][1]中。

状态转移公式为：

dp[i][j] = min(dp[i+1][j+1],dp[i+1][j]) + triangle[i][j]

下面是dp数组变化的动图演示：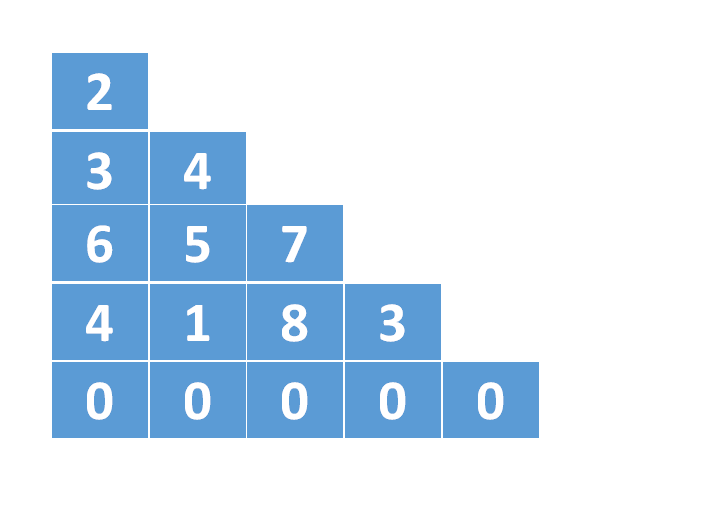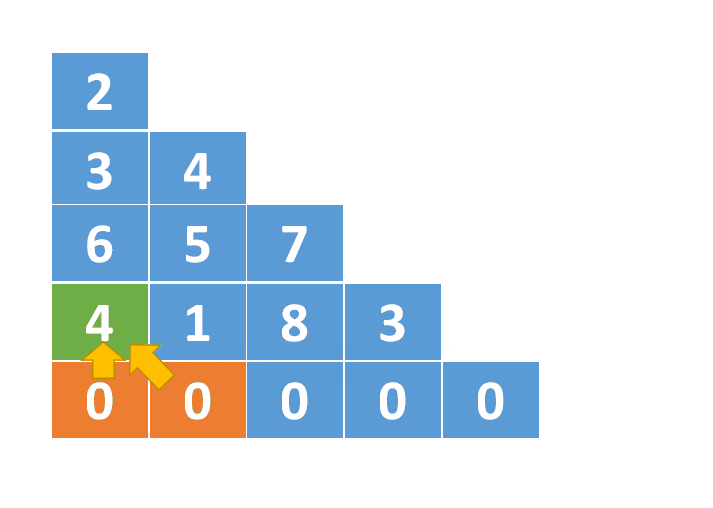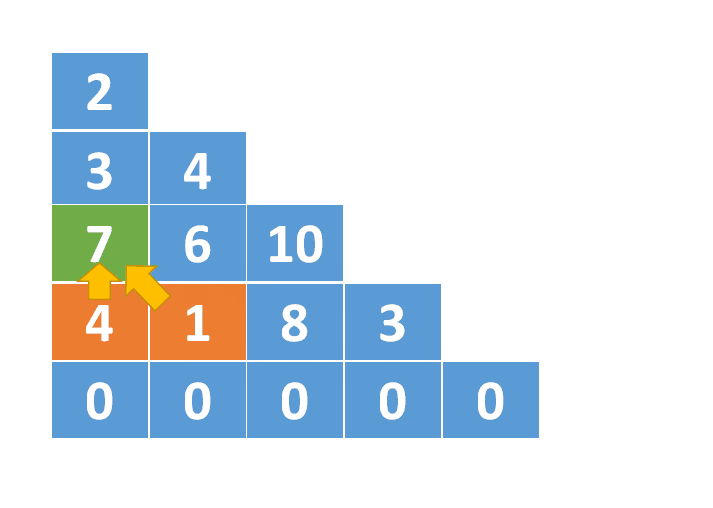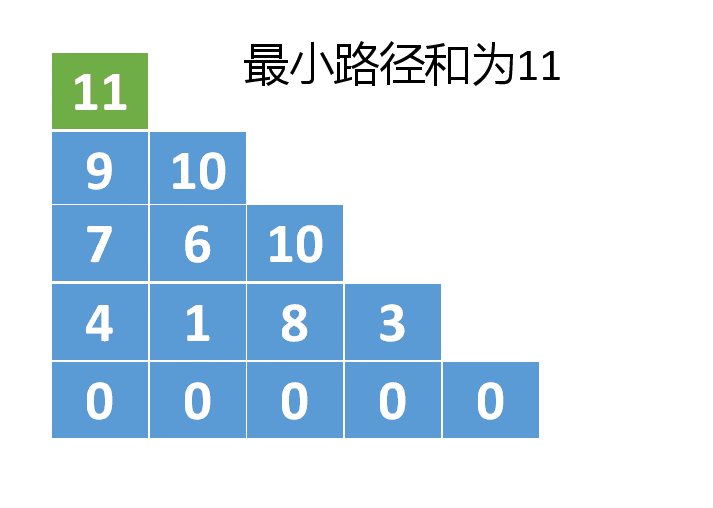
代码实现：

/**
 * @param {number[][]} triangle
 * @return {number}
 */
/**
 * @param {number[][]} triangle
 * @return {number}
 */
var minimumTotal = (triangle) => {
  const n = triangle.length;
  // 初始化dp数组
  const dp = new Array(n);
  for (let i = 0; i < n; i++) {
    dp[i] = new Array(triangle[i].length);
  }
  for (let i = n - 1; i >= 0; i--) { // 自底而上遍历
    for (let j = 0; j < triangle[i].length; j++) { // 同一层的
      if (i == n - 1) { // base case 最底层
        dp[i][j] = triangle[i][j];
      } else { // 状态转移方程，上一层由它下面一层计算出
        dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle[i][j];
      }
    }
  }
  return dp[0][0];
};

参考：https://leetcode-cn.com/problems/triangle/solution/san-chong-jie-fa-duo-tu-xiang-jie-120-san-jiao-xin/