题目

题目来源：力扣（LeetCode）

返回 A 的最短的非空连续子数组的长度，该子数组的和至少为 K 。
如果没有和至少为 K 的非空子数组，返回 -1 。

示例 1：

输入：A = [1], K = 1
输出：1

示例 2：

输入：A = [1,2], K = 4
输出：-1

示例 3：

输入：A = [2,-1,2], K = 3
输出：3

思路分析

连续子数组的和经典求法: 前缀和, 用preSum[i]表示数组A[0]到A[i - 1]的和, 那么子数组i到j-1的和可以表示为preSum[j] - preSum[i];

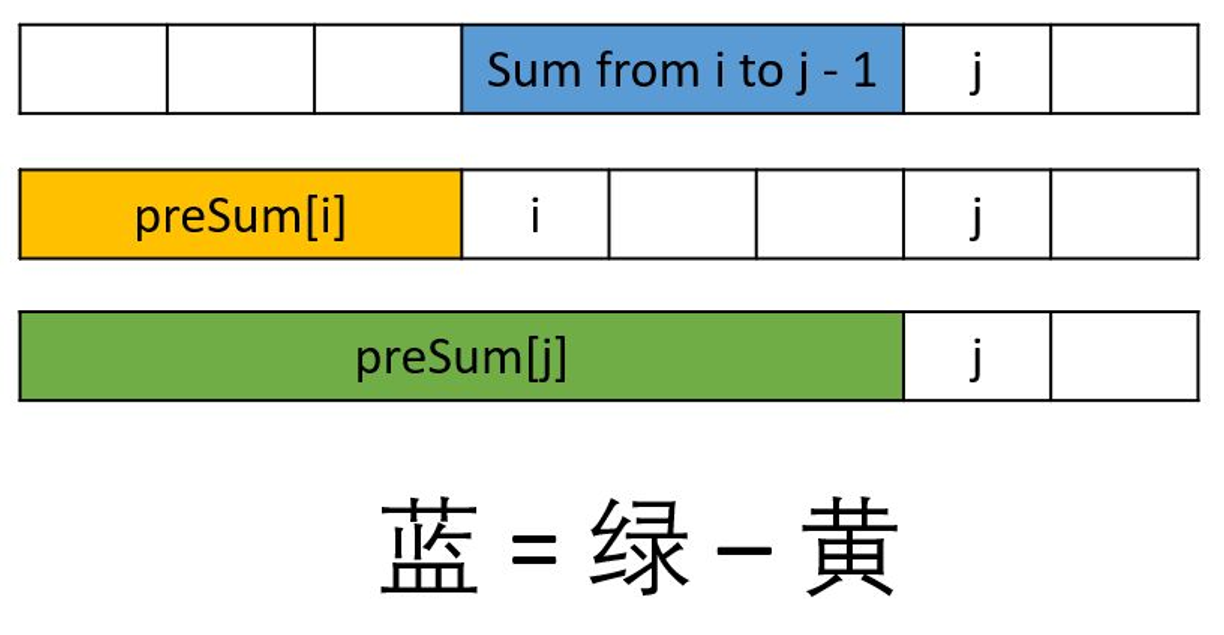
image.png

具体地，维护一个递增的单调队列（因为要求和至少为 KK 的最短子数组的长度，所以队列中存储的是元素的下标）。
维护好一个单调递增的队列，队首元素就是最小值，即队首元素是当前遇到的所有区间和中最小的（因为这样才能在当前遍历的区间 [0, i−1] 的和 减去 之前遍历过的最小的区间和才会尽可能的得到满足条件的差值，即满足条件的区间和，每找到一个符合条件的区间就比较一次区间长度，记录最短子数组的长度）。

  1. var shortestSubarray = function (A, K) {
  2.   // 初始化一个数组，其长度为 原数组A的长度，初始值都为 0
  3.   const preSum = new Array(A.length + 1).fill(0);
  4.   // 求出原数组A 的前缀和数组的值
  5.   for (let i = 0; i < A.length; i++) {
  6.     preSum[i + 1] = preSum[i] + A[i];
  7.   }
  9.   // 维护一个单调递增的单调队列 (由于要求和至少为 K 的最短子数组的长度，所以实际上队列中存储的是原数组A中元素的下标)
  10.   let queue = [];
  11.   let minLen = A.length + 1;
  13.   for (let j = 0; j < preSum.length; j++) {
  15.     // 若当前遍历的前缀和 preSum[j] （即区间 [0, j - 1]） <= 以当前队尾元素为下标的前缀和 preSum[queue[queue.length - 1]] (即上一次的前缀和，其区间为 [0， queue.pop() - 1])
  16.     // 此时队尾元素出队
  17.     while (queue.length != 0 && preSum[queue[queue.length - 1]] >= preSum[j]) {
  18.       queue.pop()
  19.     }
  20.     // 若当前遍历的前缀和 sum[i]sum[i]（即区间 [0, i - 1][0,i−1]） -− 以当前队头元素为下标的前缀和 sum[q.peekFirst()]sum[q.peekFirst()]（即区间 [0, q.peekFirst() - 1][0,q.peekFirst()−1]）
  21.     // （二者相减即为区间 [q.peekFirst(), i - 1][q.peekFirst(),i−1] 的和）>= K>=K，说明该区间的和满足条件，此时更新 minLengthminLength。
  23.    // 若当前遍历的前缀和 preSum[j] (即区间 [0, j - 1]) - 以当前队首元素为下标的前缀和 preSum[queue[0]] (即区间 [0, queue.shift() - 1]) >= K
  24.    // 说明该区间的和 (二者相减即为区间 [queue.shift(), j - 1][queue.shift(),i − 1] 的和)满足条件，此时更新最小长度 minLen
  25.     while (queue.length != 0 && preSum[j] - preSum[queue[0]] >= K) {
  26.       minLen = Math.min(j - queue[0], minLen);
  27.       queue.shift();
  28.     }
  29.     // 更新 minLen 后，将当前遍历的下标加入单调递增的队列中
  30.     queue.push(j)
  31.   }
  33.   return minLen < A.length + 1 ? minLen : -1
  34. }