题目

题目来源：力扣（LeetCode）

给定 N，想象一个凸 N 边多边形，其顶点按顺时针顺序依次标记为 A[0], A[i], …, A[N-1]。

假设您将多边形剖分为 N-2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

示例 1：

输入：[1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：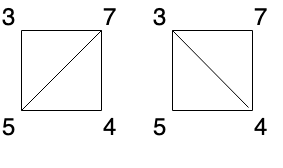
image.png
输入：[3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：375 + 457 = 245，或 345 + 347 = 144。最低分数为 144。

示例 3：

输入：[1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 113 + 114 + 115 + 111 = 13。

思路分析

  1. 3个点构成1个三角形
  2. 4个点构成1 + 1个三角形
  3. 5个点构成1 + 2 或 1 + 1 + 1 = 3个三角形
  4. 6个点构成1 + 3 或 1 + 1 + 2 = 4个三角形
  5. 7个点构成1 + 4 或 1 + 1 + 3 或1 + 2 + 2 = 5个三角形

代码实现

  1. /**
  2.  * 这道题目的关键是:
  3.  * 可以把任何顶点数大于3的凸多边形分解为一个三角形和至多两个凸多边形，并且按这种
  4.  * 方式分割，最后n个顶点得到的一定是n - 2个三角形（我不知道最后得到的一定是n - 2个三角形怎么证明
  5.  * ）。
  6.  * 那么这个就可以dp了
  7.  * @param {number[]} values
  8.  * @return {number}
  9.  */
  11. var minScoreTriangulation = function (values) {
  12.   const len = values.length
  13.   const dp = new Array(len)
  14.   // 因为dp求的是最小值，那么初始化为最大值
  15.   for (let i = 0; i < len; i++) dp[i] = new Array(len).fill(Infinity)
  16.   for (let i = 0; i < len; i++) {
  17.     // 顶点数小于3不能构成三角形，dp中不会有用到顶点数为1的情况。
  18.     //i、j包含顶点数小于2的情况的值都初始化为0,便于后面计算
  19.     dp[i][(i + 1) % len] = 0
  20.   }
  21.   // temp_len + 1代表凸多边形的顶点个数
  22.   // dp先求凸多边形有3个定点的情况，再求有4个顶点的情况下，直至求出有length个顶点的情况
  23.   for (let temp_len = 2; temp_len < len; temp_len++) {
  24.     // 这些顶点中第一个顶点是i，最后一个顶点是j。
  25.     // i和j都有可能为0 ~ (len - 1)（开闭区间）中的任何一个点
  26.     for (let i = 0; i < len; i++) {
  27.       let j = (i + temp_len) % len
  28.       // 虽然是循环的，但可以认为j在i的后面，也就是k永远不可能等于i或j
  29.       for (let k = (i + 1) % len; k !== j; k = (k + 1) % len) {
  30.         dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[k] * values[j])
  31.       }
  32.     }
  33.   }
  34.   return dp[0][len - 1]
  35. };