题目

题目来源：力扣（LeetCode）

给你二叉搜索树的根节点 root ，该树中的两个节点被错误地交换。请在不改变其结构的情况下，恢复这棵树。

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗？


示例 1：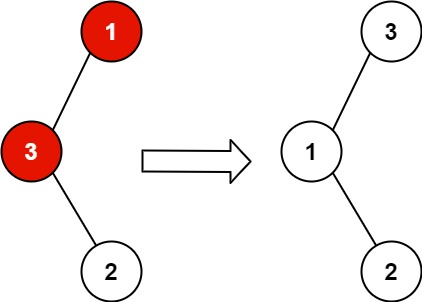
image.png

输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：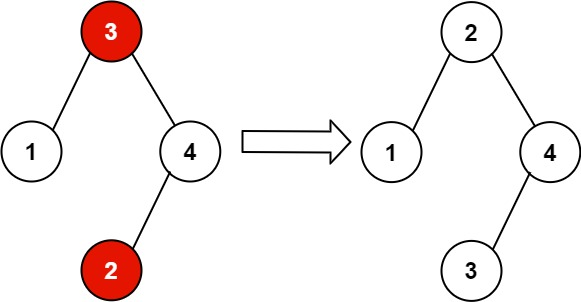
image.png

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

思路分析

Morris 中序遍历

Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：

  1. 如果 x 无左孩子，则访问 x 的右孩子，即 x = x.right。
  2. 如果 x 有左孩子，则找到 x 左子树上最右的节点（即左子树中序遍历的最后一个节点，x 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。
    • 如果 predecessor 的右孩子为空，则将其右孩子指向 x，然后访问 x 的左孩子，即 x = x.left。
    • 如果 predecessor 的右孩子不为空，则此时其右孩子指向 x，说明我们已经遍历完 xx的左子树，我们将 predecessor 的右孩子置空，然后访问 x 的右孩子，即 x = x.right。
  3. 重复上述操作，直至访问完整棵树。

其实整个过程我们就多做一步：将当前节点左子树中最右边的节点指向它，这样在左子树遍历完成后我们通过这个指向走回了 xx，且能再通过这个知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {void} Do not return anything, modify root in-place instead.
  12.  */
  13. const swap = (x, y) => {
  14.   const temp = x.val;
  15.   x.val = y.val;
  16.   y.val = temp;
  17. }
  19. var recoverTree = function (root) {
  20.   // x、y 用来记录两个被错误交换的两个节点
  21.   let x = null, y = null,
  22.   // 记录中序遍历当前节点的前驱
  23.    pred = null, 
  24.   //  用来完成 Morris 连接的寻找前驱的指针
  25.    predecessor = null;
  27.   while (root !== null) {
  28.     // 左子树不为空
  29.     // 1、连接 root 节点的前驱，它的前驱还没访问，所以 root 不能现在访问，继续访问它的左子树
  30.     // 2、root节点访问，并且断开root节点的前驱连接，然后访问root的右子树
  31.     if (root.left !== null) {
  32.       // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
  33.       predecessor = root.left;
  34.       while (predecessor.right !== null && predecessor.right !== root)
  35.         predecessor = predecessor.right;
  37.       // 让 predecessor 的右指针指向 root，继续遍历左子树
  38.       if (predecessor.right === null) {
  39.         predecessor.right = root;
  40.         root = root.left;
  41.       }
  42.       // 说明左子树已经访问完了，我们需要断开链接
  43.       else {
  44.         // 访问 root 节点
  45.         if (pred !== null && root.val < pred.val) {
  46.           y = root;
  47.           if (x === null) {
  48.             x = pred;
  49.           }
  50.         }
  51.         // 更新前驱，为下一个节点做准备
  52.         pred = root;
  53.         // 断开前驱连接
  54.         predecessor.right = null;
  55.         // 访问右子树
  56.         root = root.right;
  57.       }
  58.     }
  59.     // 如果没有左孩子，则直接访问右孩子
  60.     // root不需要链接节点的前驱（他的前驱其实就是pred(第一个节点pred为null)，且已经被访问过了），那么直接访问root
  61.     else {
  62.       if (pred !== null && root.val < pred.val) {
  63.         y = root;
  64.         if (x === null) {
  65.           x = pred;
  66.         }
  67.       }
  68.       // 更新前驱，为下一个节点作准备
  69.       pred = root;
  70.       // 访问 root 的右子树
  71.       root = root.right;
  72.     }
  73.   }
  74.   swap(x, y);
  75. };

中序遍历

  1. 把二叉搜索树看成有序序列，在有序序列里面，找到被调换的两个节点
  2. 就等价于交换有序序列的值，当后面的值小于前面的值(任意位置)，就是特殊位置，中序遍历二叉 树，找到两个后面值比前面值小的位置 ```javascript /**
  • Definition for a binary tree node.
  • function TreeNode(val, left, right) {
  • this.val = (val===undefined ? 0 : val)
  • this.left = (left===undefined ? null : left)
  • this.right = (right===undefined ? null : right)
  • } / /*
  • @param {TreeNode} root
  • @return {void} Do not return anything, modify root in-place instead. */ // pre记录前一个值，p指向第一个值，q指向最后一个值。p 和 q都是指向两个被交换的节点 let pre, p, q; var inorder = function (root) { if (root == null) return; inorder(root.left); // 从小到大依次访问每一个节点 // 当前值小于前一个值 if (pre && root.val < pre.val) { // p指向第一个值 if (p == null) p = pre; // q指向最后一个值 q = root; } // 把前一个节点更新为root pre = root; inorder(root.right); return; }; var recoverTree = function (root) { pre = p = q = null; inorder(root); // 交换p 和 q的值 let temp; temp = p.val; p.val = q.val; q.val = temp; return; }; ```

参考： https://leetcode-cn.com/problems/recover-binary-search-tree/solution/san-chong-jie-fa-xiang-xi-tu-jie-99-hui-fu-er-cha-/