计数质数

题目

题目来源：力扣（LeetCode）

统计所有小于非负整数 n 的质数的数量。

示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：0

思路分析

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。 — 百度百科

枚举

举每个数字是否为素数。判断素数的方法参考定义，对于某个数字 n，i 从 2 开始枚举判断是否满足 n % i == 0 ，如果找到了 n 的因子，就返回 false。注意 i 遍历到最大 根号n (sqrt(n)) 即可。因为 n 如果不是素数，那么至少有一个因子是小于等于 根号n (sqrt(n)) 的（如果某个因子 x >= sqrt(n)，那么 n/x <= x，而 n/x 也是 n 的因子）。

const isPrime = (x) => {
    for (let i = 2; i * i <= x; ++i) {
        if (x % i == 0) {
            return false;
        }
    }
    return true;
}
var countPrimes = function(n) {
    let ans = 0;
    for (let i = 2; i < n; ++i) {
        ans += isPrime(i);
    }
    return ans;
};

埃氏筛

埃拉托斯特尼筛法，简称埃氏筛或爱氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于根号n的所有素数的倍数剔除，剩下的就是素数。 — 百度百科

给出要筛数值的范围n，找出以内的素数。先用2去筛，即把2留下，把2的倍数剔除掉；再用下一个质数，也就是3筛，把3留下，把3的倍数剔除掉；接下去用下一个质数5筛，把5留下，把5的倍数剔除掉；不断重复下去……。

具体方法如下：

初始化长度 O(n) 的标记数组，表示这个数组是否为质数。数组初始化所有的数都是质数.
从 2 开始将当前数字的倍数全都标记为合数。标记到根号n 即 sqrt(n) 时停止即可。具体可以看来自维基百科的动画：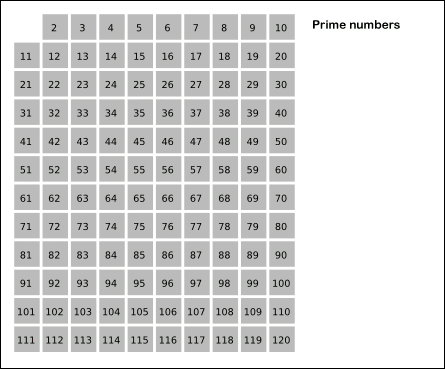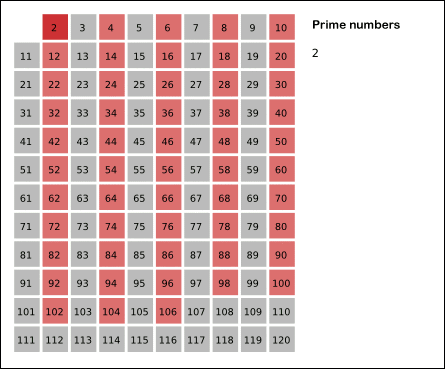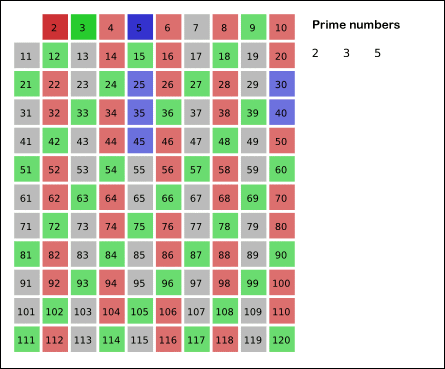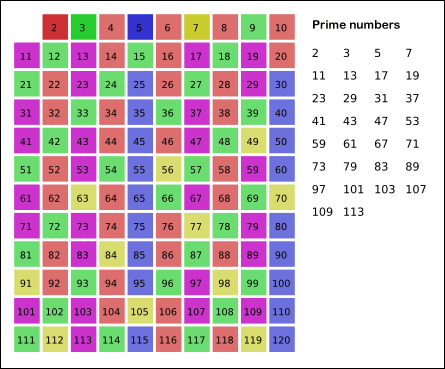

注意每次找当前素数 x 的倍数时，是从 x^2 开始的。因为如果 x > 2，那么 2 * x 肯定被素数 2 给过滤了，最小未被过滤的肯定是 x^2 。

为什么遍历的时候从 x * x 开始呢？

任意素数x的倍数有：2x, 3x, 4x, …, xx, (x+1)x, …
任意小于xx的倍数都被之前的素数筛过滤过，如：2 过滤 2x, 4x, …，3 过滤 3x, …
所以从xx开始过滤之后的倍数，所以x只需遍历到sqrt(N)

/**
 * @param {number} n
 * @return {number}
 */
var countPrimes = function (n) {
  const isPrime = new Array(n).fill(1);
  let ans = 0;
  // 从 2 开始枚举到 sqrt(n)
  for (let i = 2; i < n; ++i) {
    // 如果当前是素数
    if (isPrime[i]) {
      // 计数
      ans += 1;
      // 就把从 i*i 开始，i 的所有倍数都设置为 false。
      for (let j = i * i; j < n; j += i) {
        isPrime[j] = 0;
      }
    }
  }
  return ans;
};