题目

题目来源：力扣（LeetCode）

n 块石头放置在二维平面中的一些整数坐标点上。每个坐标点上最多只能有一块石头。
如果一块石头的 同行或者同列 上有其他石头存在，那么就可以移除这块石头。

给你一个长度为 n 的数组 stones ，其中 stones[i] = [xi, yi] 表示第 i 块石头的位置，返回 可以移除的石子 的最大数量。

示例 1：

输入：stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
输出：5
解释：一种移除 5 块石头的方法如下所示：
1. 移除石头 [2,2] ，因为它和 [2,1] 同行。
2. 移除石头 [2,1] ，因为它和 [0,1] 同列。
3. 移除石头 [1,2] ，因为它和 [1,0] 同行。
4. 移除石头 [1,0] ，因为它和 [0,0] 同列。
5. 移除石头 [0,1] ，因为它和 [0,0] 同行。
石头 [0,0] 不能移除，因为它没有与另一块石头同行/列。

示例 2：

输入：stones = [[0,0],[0,2],[1,1],[2,0],[2,2]]
输出：3
解释：一种移除 3 块石头的方法如下所示：
1. 移除石头 [2,2] ，因为它和 [2,0] 同行。
2. 移除石头 [2,0] ，因为它和 [0,0] 同列。
3. 移除石头 [0,2] ，因为它和 [0,0] 同行。
石头 [0,0] 和 [1,1] 不能移除，因为它们没有与另一块石头同行/列。

示例 3：

输入：stones = [[0,0]]
输出：0
解释：[0,0] 是平面上唯一一块石头，所以不可以移除它。

思路分析

根据题意，我们可以把二维坐标上的石头想象成是图的定点，如果两个石头的横坐标或者纵坐标相同，那么在它们之间可以形成一条线。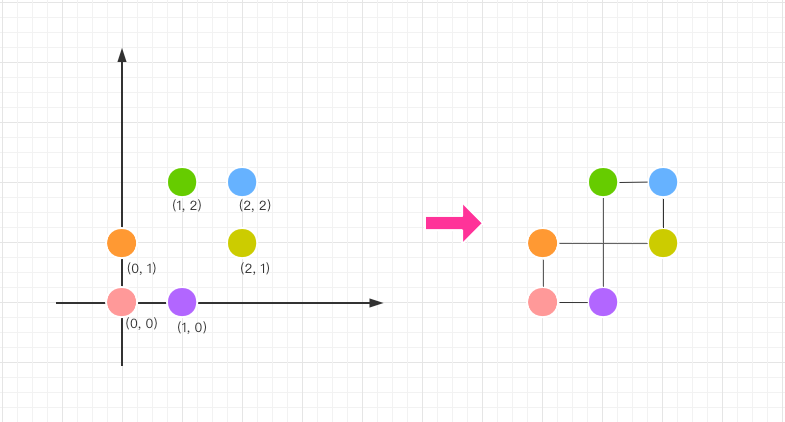
image.png
可以发现，只要是处于同一横坐标或处于同一纵坐标的石头，我们就可以将其看作是相互连通的，因此可以将处于同一横坐标或者同一坐标的石头合并成一块。但所有石头合并完之后，所有石头的个数减去连通分量的个数的结果就是最多可以移除的石头个数。

我们建立一个并查集，每次取两个石头的坐标，然后进行判断，如果两块石头处于同一横坐标或者同一纵坐标，那么我们就进行合并，直到遍历完整个石头的数组。每合并一次就会减少一个石头，最后所剩下的石头个数就是连通分量的个数，所以：最多可以移除的石头的个数 = 所有石头的个数 - 连通分量的个数。

  1. /**
  2.  * @param {number[][]} stones
  3.  * @return {number}
  4.  */
  5. var removeStones = function (stones) {
  6.   let stoneNum = stones.length; // 石头的数量
  7.   let uf = new UnionFind(stoneNum); //以石头个数为大小的并查集
  8.   for (let i = 0; i < stoneNum; i++) { // 首先取第一个石头
  9.     for (let j = i + 1; j < stoneNum; j++) { // 拿第二块石头
  10.       let [x1, y1] = stones[i]; // 第一块石头的第0个值，第一个值
  11.       let [x2, y2] = stones[j]; // 拿一块石头和后面石头的坐标
  12.       if (x1 == x2 || y1 == y2) { // 如果两块石头的横坐标或纵坐标是相同的，可以认为它们是连通的，将它们进行合并
  13.         uf.unite(i, j);
  14.       }
  15.     }
  16.   }
  17.   return stoneNum - uf.getCount(); // 原先的石头数量 - 合并完之后的石头数量(连通分量的个数) = 销毁的石头数量
  18. };
  21. // 并查集
  22. class UnionFind {
  23.   constructor(n) {
  24.     // 元素所指向的父节点，parent[i] 表示第 i 个元素所指向的父节点
  25.     // 初始化时, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
  26.     this.parent = new Array(n).fill(0).map((value, index) => index);
  27.     // 树的层数，rank[i] 表示以 i 为根的集合所表示的树的层数
  28.     this.rank = new Array(n).fill(1);
  29.     // 节点的个数
  30.     this.setCount = n;
  31.   }
  33.   // 查找过程，查找元素 index 所在集合的编号(查找树的根节点)
  34.   findSet(index) {
  35.     // 不断去查询自己的父节点，直至根节点
  36.     // 根节点的标志是父节点就是本身  parent[index] == index
  37.     if (this.parent[index] != index) {
  38.       // 递归获取节点的父节点
  39.       this.parent[index] = this.findSet(this.parent[index]);
  40.     }
  41.     // 返回根节点
  42.     return this.parent[index];
  43.   }
  45.   // 合并两个集合
  46.   unite(index1, index2) {
  47.     let root1 = this.findSet(index1);
  48.     let root2 = this.findSet(index2);
  49.     // 根节点不一样，是两个不同的集合(两棵不同的树)
  50.     if (root1 != root2) {
  51.       // 根据树的层数合并集合
  52.       // 
  53.       if (this.rank[root1] < this.rank[root2]) {
  54.         // 这个判断如果 root2 所在树的层数 大于 root1，就交换两个父节点，这样始终让 root1 为父节点
  55.         [root1, root2] = [root2, root1];
  56.       }
  57.       // 将层数多的集合合并到集合少的集合
  58.       this.parent[root2] = root1;
  59.       this.rank[root1] += this.rank[root2];
  60.       this.setCount--;
  61.     }
  62.   }
  64.   getCount() {
  65.     return this.setCount;
  66.   }
  68.   connected(index1, index2) {
  69.     return this.findSet(index1) === this.findSet(index2);
  70.   }
  71. }