数据结构与算法学习之并查集

并查集

并查集是一种树形的数据结构，用于处理一些不相交集合的合并及查询问题，在使用中通常以森林来表示。

并查集的思想是用一个数组来表示整片森林，树的根节点唯一标识了一个集合，我们只要找到了某个元素的树根，就能知道它在哪个集合里。

通常情况下，用集合中的某个元素来代表这个集合，该元素称为集合的代表元。
一个集合内的所有元素组织成以代表元为根的树形结构。
对于每一个元素 parent[x]指向x在树形结构上的父亲节点。如果x是根节点，则令parent[x] = x。
对于查找操作，假设需要确定x所在的的集合，也就是确定集合的代表元。可以沿着parent[x]不断在树形结构中向上移动，直到到达根节点。

例如在下面的一组元素中，每个元素代表一个集合，用 parent 表示当前元素指向的父节点，每个元素指向自己，所以它们都是这个集合中的根节点。

并查集解决的问题

并查集用在一些有 N 个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，期间要反复查找一个元素在哪个集合中。这个过程看似并不复杂，但数据量极大，若用其它的数据结构来描述的话，往往在空间上过大，计算机无法承受，也无法在短时间内计算出结果，所以只能用并查集来处理。

初始化

class UnionFind {
  constructor(n) {
    this.parent = new Array(n).fill(0).map((value, index) => index);
    this.rank = new Array(n).fill(1);
    this.setCount = n;
  }
}

定义一个 UnionFind 类，在该类的构造函数 constructor 中分别定义 parent、rank、setCount 三个属性。其中：

• parent：表示元素所指向的父节点，那么 parent[i] 表示的是第 i 个元素所指向的父节点
• rank：表示树的层数，那么 rank[i] 表示的是以 i 为根的集合所表示的树的层数
• setCount：表示节点的个数

在初始化时，每个 parent[i] 指向自己，表示每一个元素自己自成一个集合，此时 i 为根节点。每个以 i 为根的集合所表示的树的层数为 1 。

查找

// 查找元素 index 所对应的集合编号
findSet(index) {
  // 不断去查询自己的父节点，直至根节点
  // 根节点的标志是父节点就是本身  parent[index] == index
  if (this.parent[index] != index) {
    // 递归获取子节点的父节点
    this.parent[index] = this.findSet(this.parent[index]);
  }
  return this.parent[index];
}

在查找某个元素所对应的集合时，通过递归的方式一层一层地访问父节点，直至根节点 (根节点的标志就是父节点是本身) 。

合并

unite(index1, index2) {
  let root1 = this.findSet(index1), root2 = this.findSet(index2);
  if (root1 != root2) {
    if (this.rank[root1] < this.rank[root2]) {
      [root1, root2] = [root2, root1];
    }
    this.parent[root2] = root1;
    this.rank[root1] += this.rank[root2];
    this.setCount--;
  }
}

合并两个元素所属的集合，分别查询两个元素的根节点，使其中一个根节点指向另外一个根节点，两个集合就合并了。这个操作是 O(h) 的时间复杂度，其中 h 为树的高度。

在合并两个元素所属的集合时，更为准确的一种作法是根据两个集合的层数，具体判断根节点的指向，层数少的集合根节点指向层数多的集合根节点，这就可以确保合并后的集合所表示的树的层数是最少的。

例如在下图所表示的集合中，将以 7 为根节点的集合的根节点指向以 8 为根节点的集合：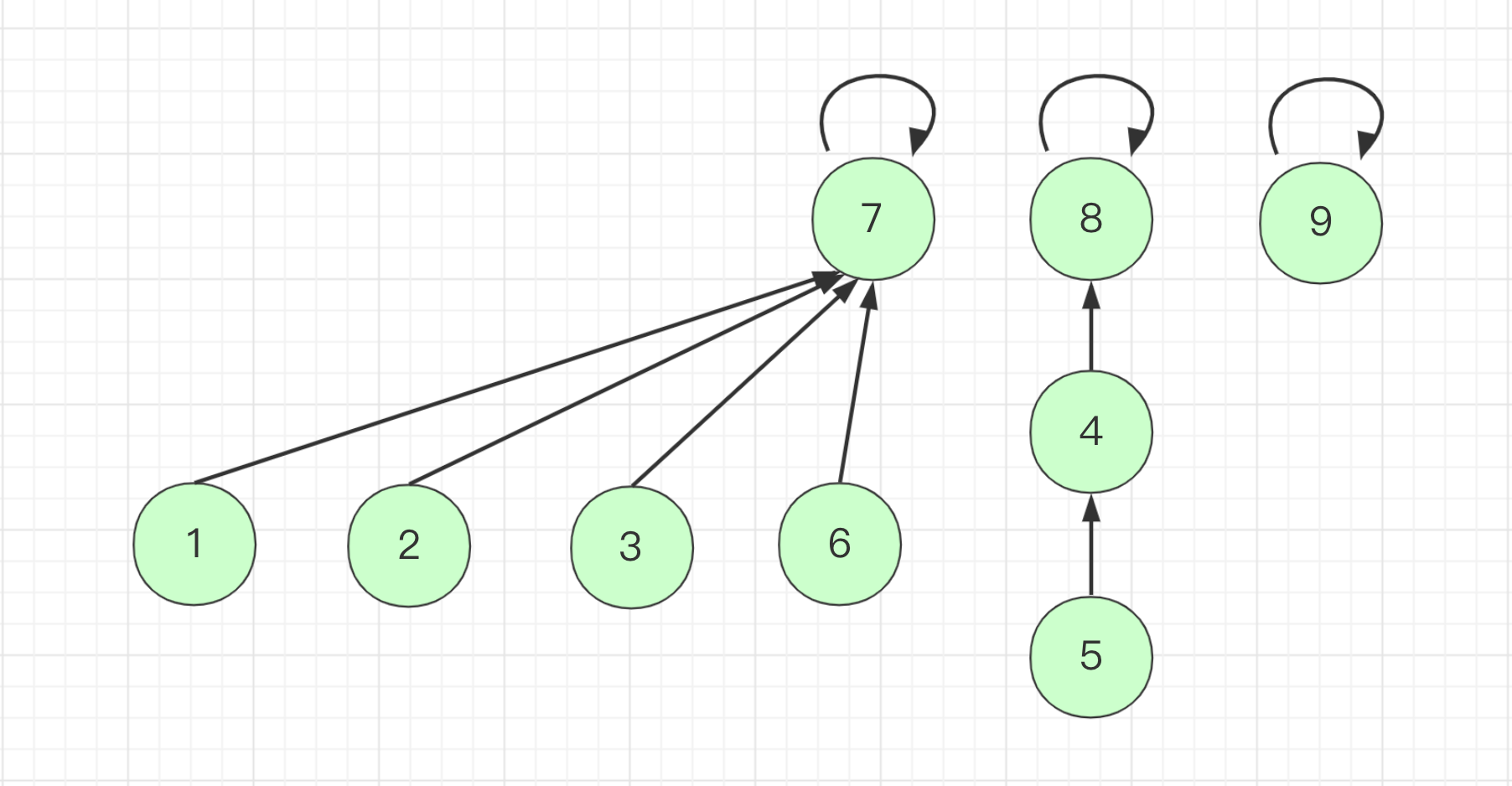

合并后的集合如下图，其所表示的树的层数是最少的：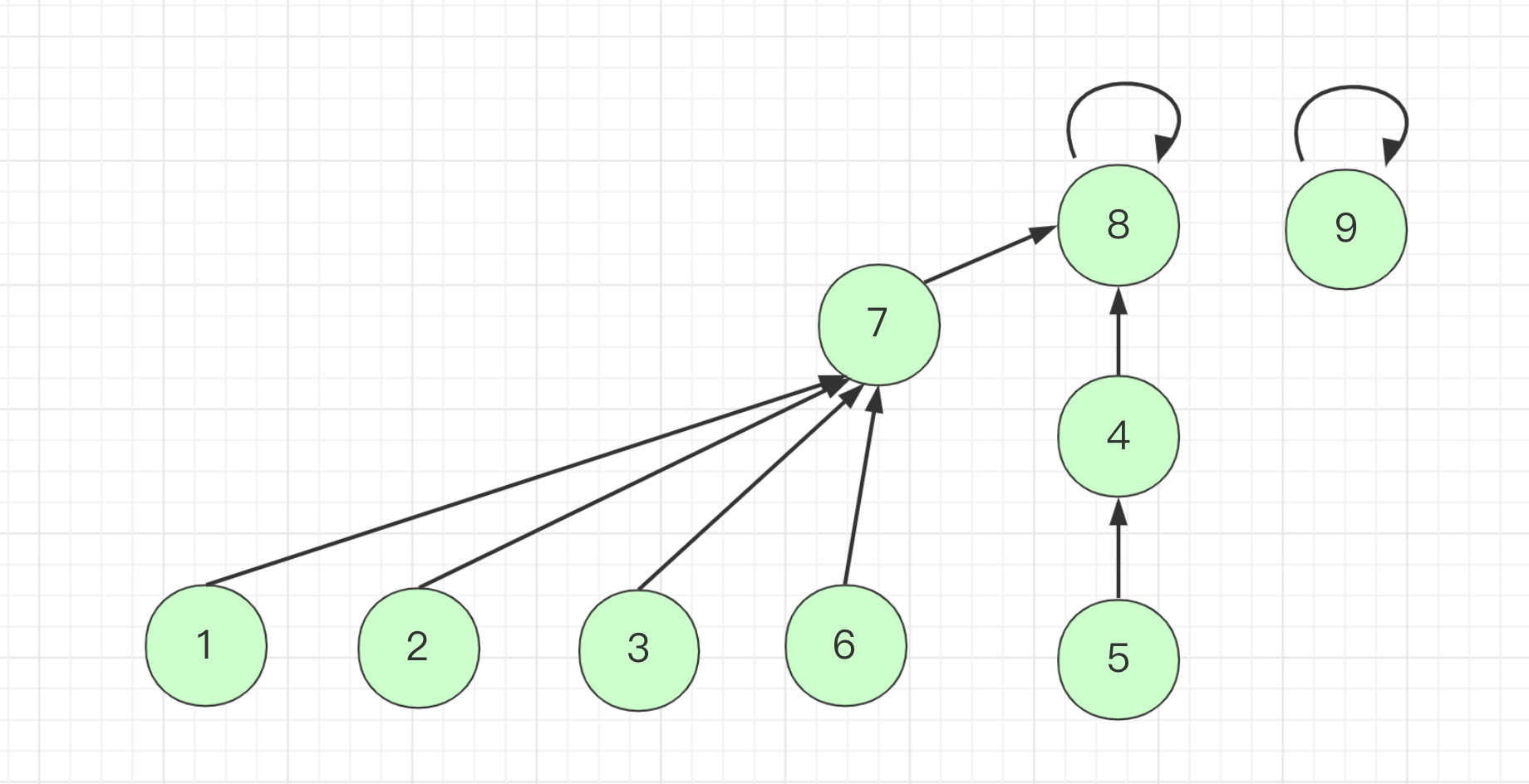

判断两个元素是否属于同一个集合

connected(index1, index2) {
  let root1 = this.findSet(index1), root2 = this.findSet(index2);
  return root1 == root2;
}

断两个元素是否属于同一个集合，只需要看它们的根节点是否相同即可。这个操作的事件复杂度为 O(h)，其中 h 为树的高度。

路径压缩

并查集里的 findSet 方法里可以进行路径压缩，是为了更快速地查找一个节点的根节点。对于一个集合树来说，它的根节点下面可以依附着许多的节点，因此，我们可以尝试在查找的过程中，从底向上，如果此时访问的节点不是根节点的话，那么我们可以把这个节点尽量的往上挪一挪，减少树的层数，这个过程就叫做路径压缩。

如下图中，findSet(5) 的过程就可以做路径压缩，让树的层数更少。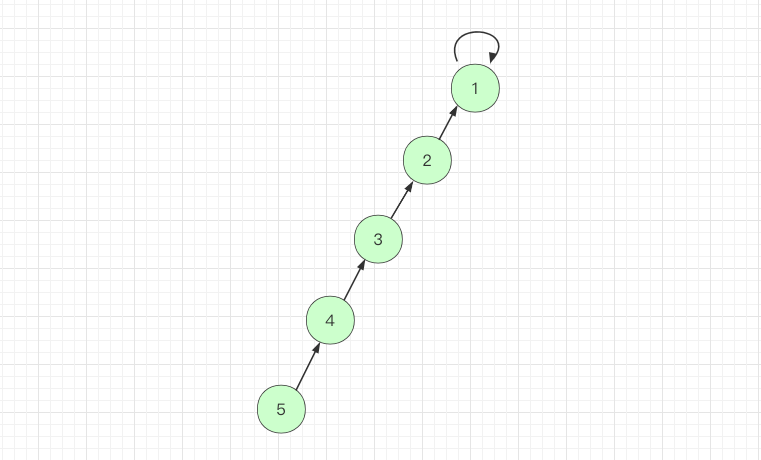

节点 5 往上寻找根节点时，把节点5指向其原来父节点的父节点，即指向节点3，树的层数就减少了一层：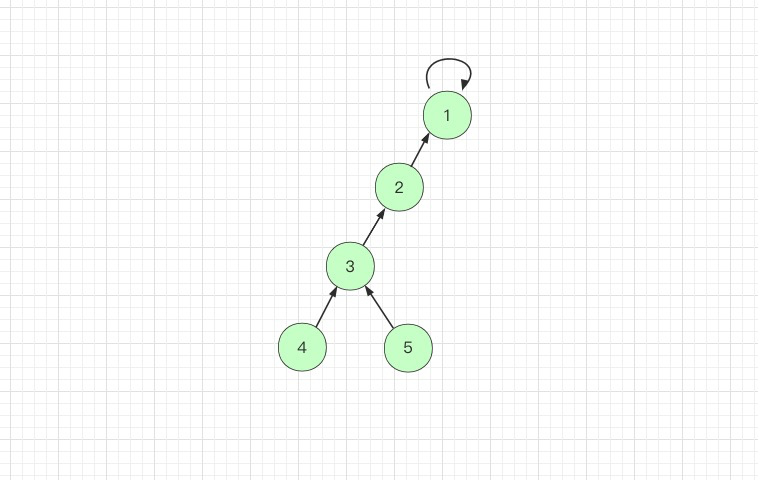

节点 3 继续往上寻找，也不是根节点，那么把节点3 指向其原来父节点的父节点，即指向节点1，树的层数减少了一层，此时节点 1 是根节点 (根节点的标志是父节点是其本身)，在 findSet 中返回根节点。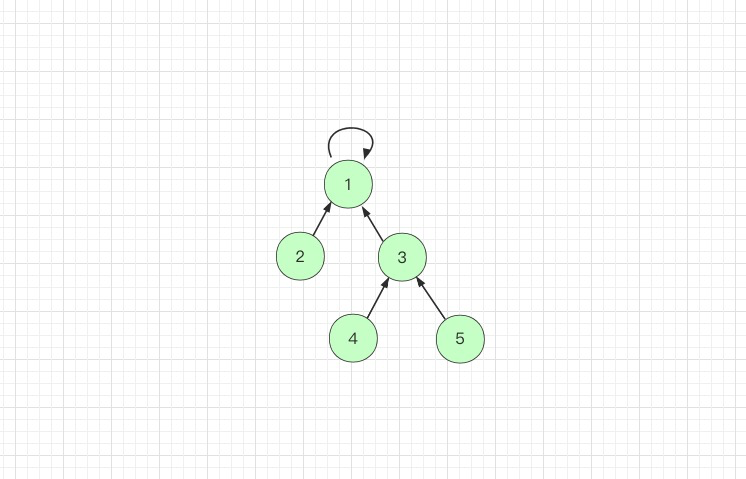

上述的路径压缩不是最优的方式，我们可以把最初的树压缩成下图所示，树的层数是最少的：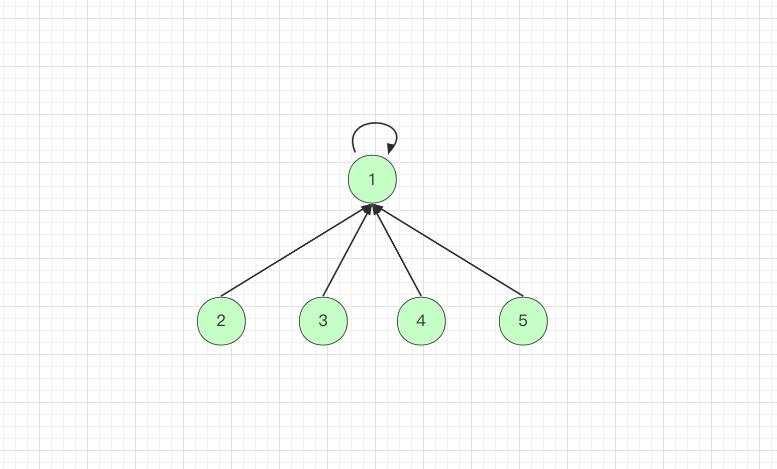

这个过程的 findSet 代码为：

findSet(index) { 
  // 路径压缩
  if (this.parent[index] !== index) {
    // 使用递归获取子节点的父节点
    this.parent[index] = this.findSet(this.parent[index]) 
  }
  // 返回根节点
  return this.parent[index]
}

完整代码

class UnionFind {
  constructor(n) {
    // 元素所指向的父节点，parent[i] 表示第 i 个元素所指向的父节点
    // 初始化时, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    this.parent = new Array(n).fill(0).map((value, index) => index);
    // 树的层数，rank[i] 表示以 i 为根的集合所表示的树的层数
    this.rank = new Array(n).fill(1);
    // 节点的个数
    this.setCount = n;
  }
  // 查找过程，查找元素 index 所在集合的编号(查找树的根节点)
  findSet(index) {
    // 不断去查询自己的父节点，直至根节点
         // 根节点的标志是父节点就是本身  parent[index] == index
    if (this.parent[index] != index) {
      // 递归获取节点的父节点
      this.parent[index] = this.findSet(this.parent[index]);
    }
    // 返回根节点
    return this.parent[index];
  }
  // 合并两个集合
  unite(index1, index2) {
    let root1 = this.findSet(index1);
    let root2 = this.findSet(index2);
    // 根节点不一样，是两个不同的集合(两棵不同的树)
    if (root1 != root2) {
      // 根据树的层数合并集合
      // 
      if (this.rank[root1] < this.rank[root2]) {
        // 这个判断如果 root2 所在树的层数 大于 root1，就交换两个父节点，这样始终让 root1 为父节点
        [root1, root2] = [root2, root1];
      }
      // 将层数多的集合合并到集合少的集合
      this.parent[root2] = root1;
      this.rank[root1] += this.rank[root2];
      this.setCount--;
    }
  }
  getCount() {
    return this.setCount;
  }
  connected(index1, index2) {
    let root1 = this.findSet(index1);
    let root2 = this.findSet(index2);
    return root1 == root2;
  }
}