计数排序

计数排序的核心在于将输入的数据值转化为存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序的特征

• 当输入的元素是 n 个 0 到 k 之间的整数，它的运行时间是 O(n + k)；
• 计数排序不是比较排序，排序的速度快于任何比较排序算法；
• 由于用来计数的数组 C 的长度取决于待排序数组中数据的范围 (等于待排序数组的最大值与最小值的差加上 1)，这使得计数排序对于数据范围很大的数组，需要大量时间和内存。

计数排序是用来排序 0 到 100 之间的数字最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

通俗地理解，例如有 10 个年龄不同的人，统计出有 8 个人的年龄比 A 小，那么 A 的年龄就排在第 9 位，用这个方法可以得到其他每个人的位置，也就排好了序。当然，年龄有重复是需要特殊处理 (保证稳定性)，这就是为什么最后要反向填充目标数组，以及将每个数字的统计减去 1 的原因。

实现步骤

1. 找出待排序的数组中最大和最小的元素；
2. 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项；
3. 对所有的计数累加 (从 C 中的第一个元素开始，每一项和前一项相加)；
4. 反向填充目标数组：将每个元素 i 放在新数组的第 C(i) 项，每放一个元素就将 C(i) 减去 1；

动图演示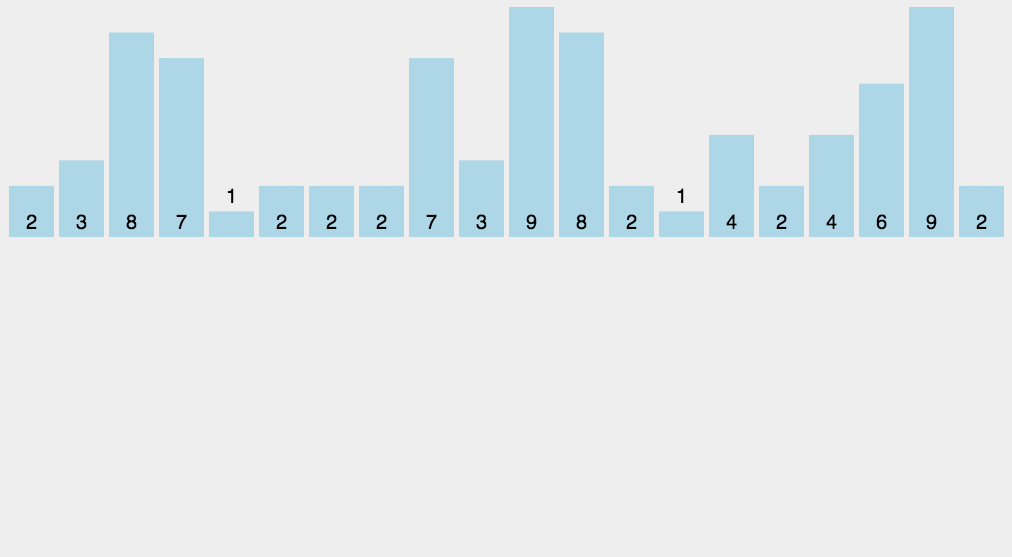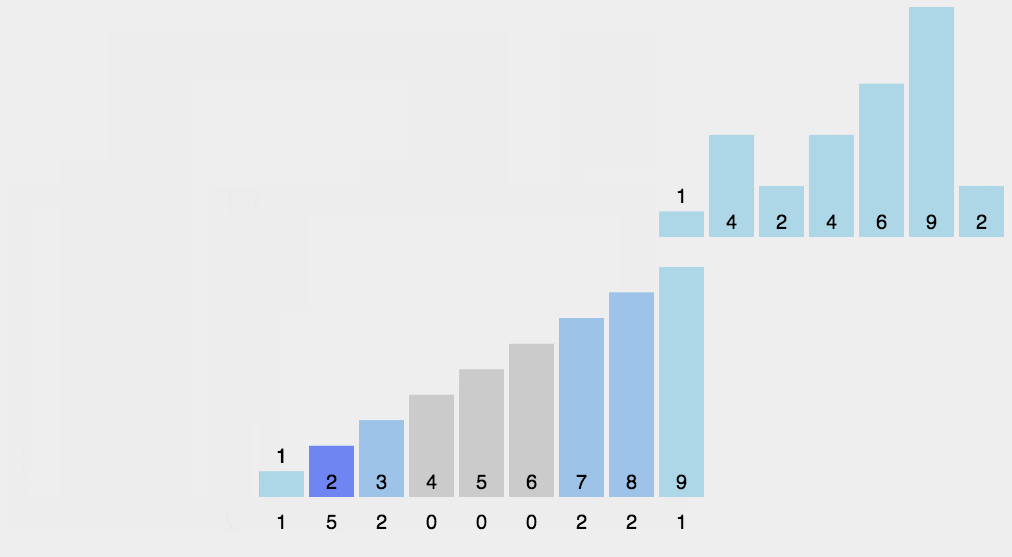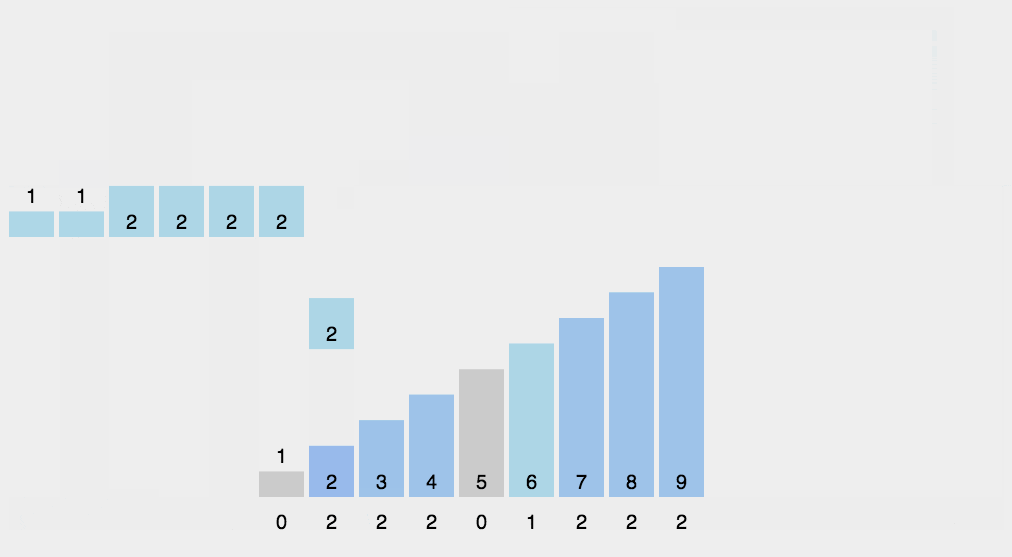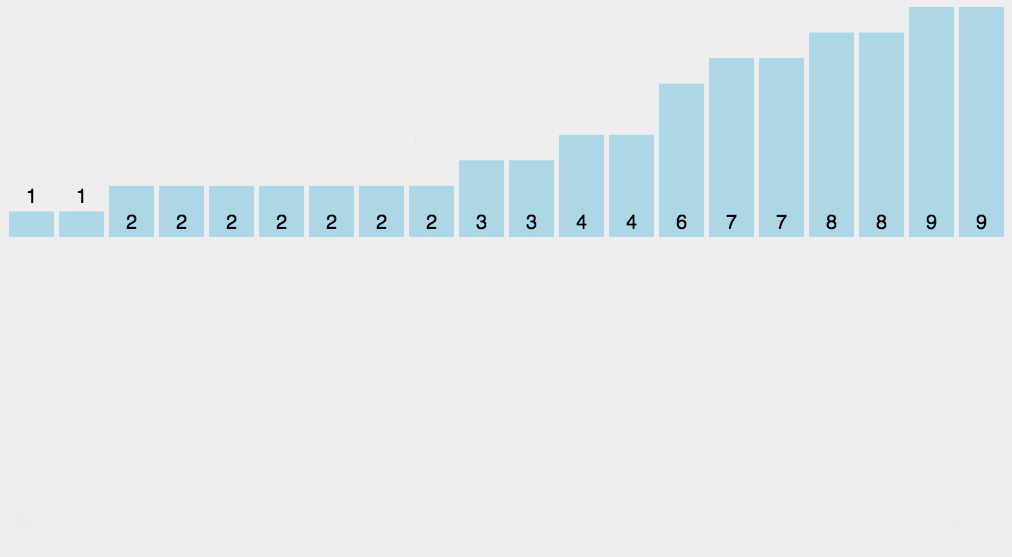

JavaScript 代码实现

function countingSort(arr, maxValue) {
    const bucket = new Array(maxValue - 1);
  let sortedIndex = 0;
  const arrLen = arr.length;
  const bucketLen = maxValue + 1;
  for (let i = 0; i < arrLen; i++) {
      if (!bucket[arr[i]]) {
        bucket[arr[i]] = 0;
    }
    bucket[arr[i]]++;
  }
  for (let j = 0; j < bucketLen; j++) {
      while(bucket[j] > 0) {
        arr[sortedIndex++] = j;
      bucket[j]--;
    }
  }
  return arr;
}