数据结构与算法学习之二叉搜索树

前言

在 数据结构与算法学习之树 一文中，我们对树的基本概念及二叉树作了简单的介绍。接下来，我们将会输入学习二叉搜索树，并使用 JavaScript 语言实现二叉搜索树这种数据结构。

二叉搜索树

二叉搜索树（Binary Search Tree），也称为 二叉查找树、有序二叉树或排序二叉树，是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不为空，则右子树上所有子节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉搜索树；

二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势，因此应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

实现二叉搜索树

下图为二叉搜索树的数据结构：

创建 Node 类

我们创建一个 Node 类来表示二叉搜索树中的每个节点：

export class Node {
    constructor(data) {
      this.data = data; // 节点值
    this.left = null; // 左侧子节点的引用
    this.right = null; // 右侧子节点的引用
  }
}

声明 Compare 常量

export const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};

创建 defaultCompare 函数

export function defaultCompare(a, b) {
  if (a === b) {
    return Compare.EQUALS;
  }
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

创建 BinarySearchTree 类

export default class BinarySearchTree {
    constructor(compareFn = defaultCompare) {
      this.compareFn = compareFn; // 用来比较节点值
    this.root = null; // 根节点
  }
}

接下来，我们会为二叉搜索树声明一些可用的方法：

insert(key) 向树中插入一个新的键
search(key) 在树中查找一个键，如果节点存在，则返回 true，若不存在，则返回 false
min() 返回树中最小的值/键
max() 返回树中最大的值/键
remove(key) 从树中移除某个键
inOrderTraverse() 通过中序遍历方式遍历所有节点
preOrderTraverse() 通过先序遍历方式遍历所有节点
postOrderTraverse() 通过后序遍历方式遍历所有节点

下面，我们逐一实现这些方法：

insert(key) 向树中插入一个新的键

insert(key) {
    if (this.root == null) {
    // 插入的是根节点
      this.root = new Node(key);
  } else {
    // 将节点添加到根节点以外的其它位置
      this.insertNode(this.root, key);
  }
}

向树中插入一个新的节点，会有两种情况。

第一种情况，插入的树节点是否为第一个节点 (根节点)，如果此时的 root 为null，则插入的是根节点，我们将创建一个 Node 类的实例并将它赋值给 root 属性来将 root 指向这个新节点。在 Node 构建函数的属性里，只需要向 Node 的构造函数传递我们想用来插入树的节点值(key)，它的左指针和右指针的值会由构造函数自动设置为 null。

第二种情况，是将节点添加到根节点以外的其它位置。在这种情况下，我们需要一个辅助方法来帮助我们做这件事，我们来定义一个 insetNode 方法。

insertNode(node, key) 添加节点到树中

insertNode(node, key) {
  // 要插入的节点的键小于父节点，则要插入的位置是左侧子节点
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
    // 父节点没有左侧子节点，则在父节点的左侧子节点位置插入新节点
      if (node.left == null) {
        node.left = new Node(key);
    } else {
      // 父节点已有左侧子节点，则继续找到树的下一层，直到找到一个没有左侧子节点的节点，然后将新节点插入到该节点的左侧子节点的位置
        this.insertNode(node.left, key);
    }
  } else {
    // 要插入的节点的键大于父节点，则要插入的位置是右侧子节点
      if (node.right == null) {
      // 父节点没有右侧子节点，则在父节点右侧子节点的位置插入新节点
        node.right = new Node(key);
    } else {
      // 父节点已有右侧子节点，则继续找到树的下一层，直到找到一个没有右侧子节点的节点，然后将新节点插入到该节点的右侧子节点的位置
        this.insertNode(node.right, key);
    }
  }
}

insertNode 方法会帮助我们找到新节点应该插入的正确位置。我们来分析一下该函数的实现逻辑：

如果树不是一颗空树，我们插入新节点时需要先找到插入的位置。我们需要从根节点开始查找，因此在调用 insertNode 时通过参数传入树的 根节点 和要插入的 新节点。

如果新节点的键小于当前节点的键（现在，当前节点就是根节点），那么我们需要检查当前节点是否有左侧子节点，如果没有，就在当前节点的左侧子节点的位置插入新节点。如果已经有左侧子节点，则需要递归调用 insertNode 方法继续找到树的下一层。在这里，下次要比较的节点将会是当前节点的左侧子节点。直到找到一个没有左侧子节点的当前节点，在当前节点的左侧子节点的位置插入新节点。

如果新插入节点的键比当前节点大（现在，当前节点是根节点），如果当前节点没有右侧子节点，就在当前节点的右侧子节点的位置插入新节点。如果已经有右侧子节点。同样需要递归调用 insertNode 方法继续找到树的下一层。此时要用来和新节点比较的节点是 右侧子节点。直到找到一个没有右侧子节点的当前节点，在当前节点的右侧位置插入新节点。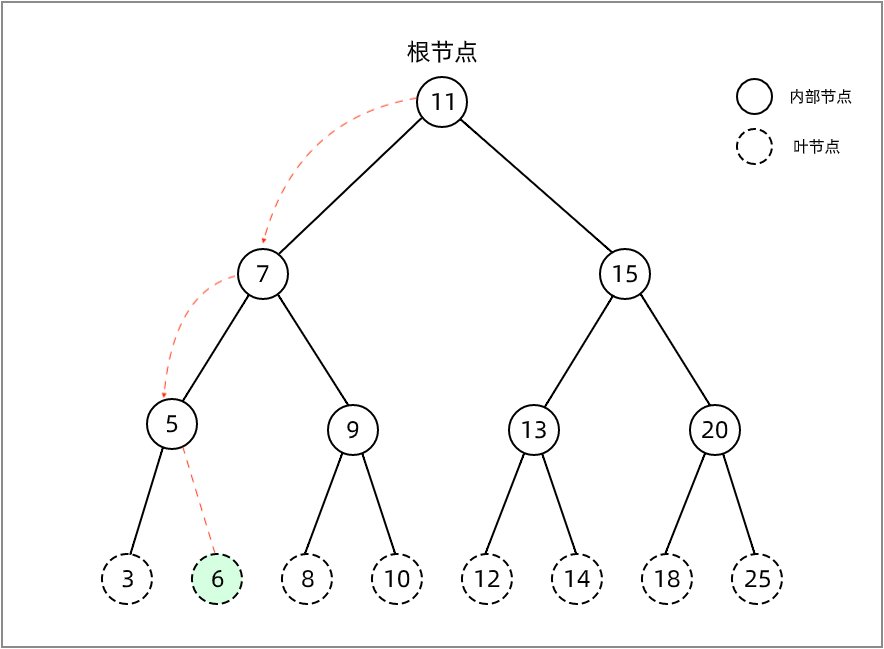

例如在一棵不为空的树中插入节点6：

1. 从根节点开始比较，节点6比根节点11小，因此查找根节点是否有左侧子节点，此时发现根节点已有左侧子节点7
2. 节点6和节点7作比较，还是比节点7小，因此继续查找节点7的左侧子节点，此时节点7也有左侧子节点5
3. 节点6和节点7的左侧子节点5作比较，节点6比节点5大，此时查找节点5是否有右侧子节点
4. 节点5没有右侧子节点，于是将节点6插入到节点5的右侧子节点的位置，成为节点5的右侧子节点

search(key) 在树中查找一个键

search(key) {
    return this.searchNode(this.root, key);
}

在 search 方法中，我们调用 searchNode 方法来查找树中的一个特定的值。接下来我们实现 searchNode 方法：

searchNode(node, key) {
  // 传入的 node不合法（node 为 null 或 undefined），返回 false，说明要找的键没有找到
    if (node == null) {
      return false;
  }
  // 要找的键比当前节点小，说明要找的键在左子树上，继续在左子树上搜索
  if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      return this.searchNode(node.left, key);
  }
  // 要找的键比当前节点大，说明要找的键在右子树上，继续在右子树上搜索
  else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      return this.searchNode(node.right, key);
  }
  // 要找的键当当前节点的键相等，返回 true，表示找到了这个键
  return true;
}

searchNode 方法可以用来寻找一棵树或其任意子树中的一个特定的值。

在开始查找前，首先需要验证传入的 node 是否合法（node 不是 null 或 undefined），如果不合法，我们返回 false，表示要找的键没有找到。

传入的 node 是合法的，比较要找的键和当前节点的大小。如果要找的键比当前的节点小，说明要找的键在左子树上，继续在左子树上搜索。如果要找的键比当前的节点大，说明要找的键在右子树上，继续在右子树上搜索。如果要找的键和当前的节点的键相等，说明找到了这个键，我们返回true。

min() 返回树中最小的值/键

min() {
    return this.minNode(this.root);
}

在 min 方法中，调用了 minNode 方法来查找树的最小值，下面，我们来实现 minNode 方法：

minNode(node) {
    let current = node;
  // 遍历树的左子树，直到找到树的最下层（最左端）
  while (current != null && current.left != null) {
      current = current.left;
  }
  return current
}

minNode 方法允许我们从树中任意一个节点开始寻找最小的键。我们可以使用它来找到一棵树或其子树中最小的键。

在二叉搜索树中，若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值，也就是说树中最小的值必定在左子树上。因此在 minNode 方法内部，我们遍历树的左边，直到找到树的最下层 (最左端)

如下图的树中，最小值在树的最左端，其值为 3：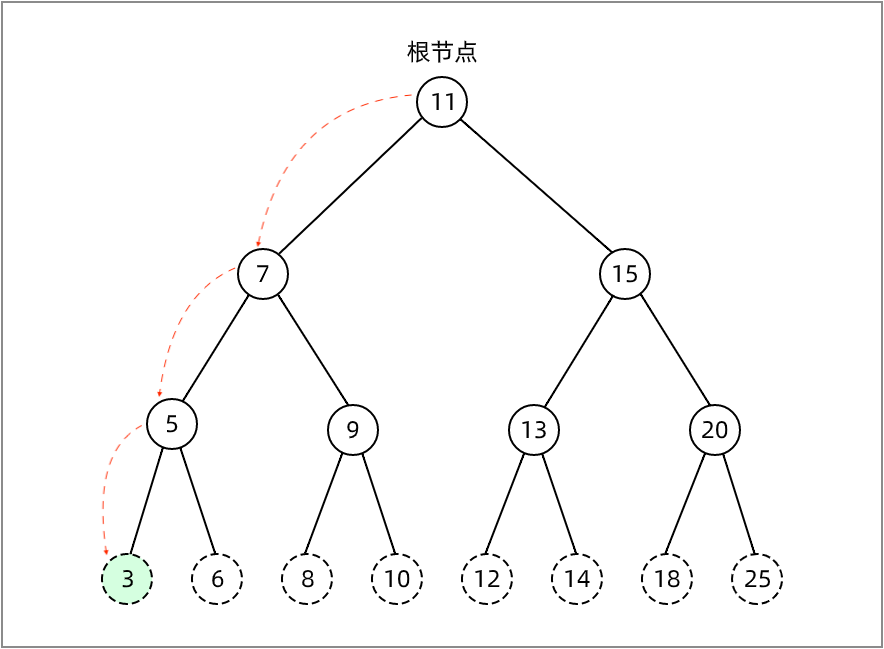

max() 返回树中最大的值/键

max() {
    return this.maxNode(this.root);
}

在 max 方法中，我们调用了 maxNode 方法来查找树中最大的值，下面我们来实现 maxNode 方法：

maxNode(node) {
    let current = node;
  // 遍历树的右子树，直到找到树的最下层（最右端）的节点
  while(current != null && current.right != null) {
      current = current.right;
  }
  return current;
}

在二叉搜索树中，若任意节点的右子树不为空，则右子树上所有子节点的值均大于它的根节点的值，即树的最大值必定在右子树上。因此，maxNode 方法会沿着树的右边进行遍历，直到找到最右端的节点。

如下图的树中，最大值在树的最右端，其值为 25：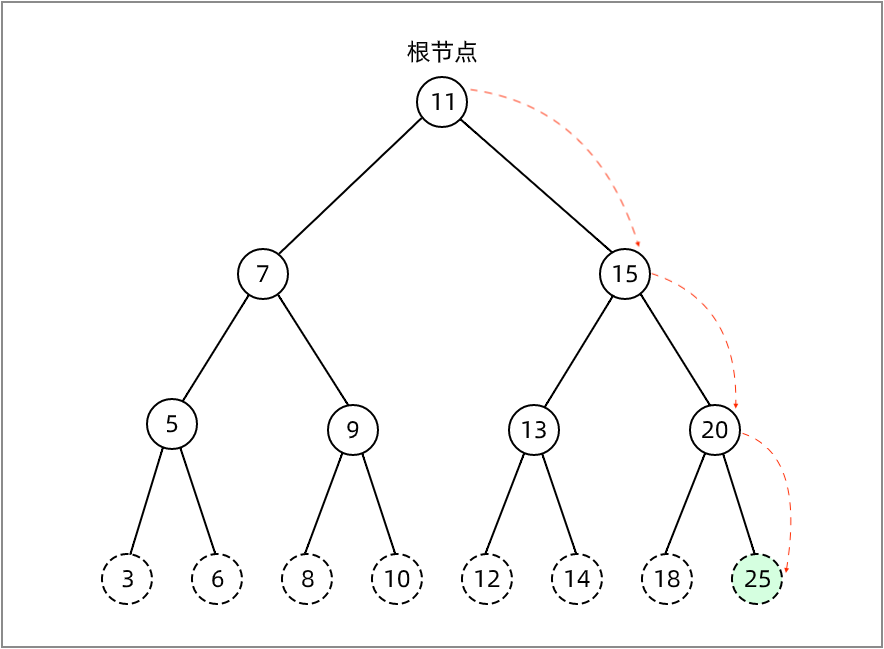

remove(key) 从树中移除某个键

remove(key) {
    this.root = this.removeNode(this.root, key);
}

在 remove 方法中调用了 removeNode 方法，传入 root 和要移除的键作为参数，并将 removeNode 方法的返回值赋值给了 root。

removeNode(node, key) {
  // 传入的节点 node 为 null，说明键不存在于树中，直接返回 null
    if (node == null) {
      return null;
  }
  // 要找的键比当前节点的值小，说明要移除的键在左子树上，沿着树的左边继续找下一个节点
  if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
    // 更新节点左指针的值
      node.left = this.removeNode(node.left, key);
    // 返回更新后的节点
    return node;
  }
  // 要找的键比当前节点的值大，说明要移除的键在右子树上，沿着树的右边继续找下一个节点
  else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
    // 更新节点右指针的值
      node.right = this.removeNode(node.right, key);
    // 返回更新后的节点
    return node;
  }
  /**
  * 找到了要移除的键，处理三种不同的情况
  * 第一种：移除一个叶节点
  * 第二种：移除一个有左侧或右侧子节点的节点
  * 第三种：移除有两个子节点的的节点
  */
  // 第一种情况
  // 移除一个叶节点（没有左侧子节点和右侧子节点）
  if (node.left == null && node.right == null) {
    // 将 节点 赋值为 null 来移除它
    node = null;
    // 返回 null 来将当前移除节点对应的父节点指针赋予 null 值
    return node;
  }
  // 第二种情况
  // 移除一个有左侧子节点或右侧子节点的节点，在这个情况下，
  // 需要跳过这个要移除的节点，直接将父节点指向该移除节点的指针指向该移除节点的子节点
  if (node.left == null) { //移除一个有右侧子节点的节点
    // 将父节点指向该移除节点的指针改为指向该移除节点的右侧子节点
    node = node.right;
    // 返回更新后的值，父节点指向移除节点的指针就会重新指向移除节点的右侧子节点
    return node;
  } else if (node.right == null) { // 移除一个有左侧子节点的节点
    // 将父节点指向该移除节点的指针改为指向该移除节点的左侧子节点
    node = node.left;
    // 返回更新后值，父节点指向移除节点的指针就会重新指向移除节点的左侧子节点
    return node;
  }
  // 第三种情况
  // 移除有左侧子节点和右侧子节点的节点
  // 找到移除节点的右子树中最小的节点
  const aux = this.minNode(node.right);
  // 将右子树中最小节点的键去更新移除节点的值，也就是改变移除节点的键，说明移除节点被删除了
  node.key = aux.key;
  // 右子树中最小的节点移至移除节点的位置后，将右子树中最小的节点删除，树中不能有两个相同键的节点
  // 然后将删除最小节点后的右子树赋值给移除节点的位置的右指针
  node.right = this.removeNode(node.right, aux.key);
  // 返回更新后的节点，移除节点的父节点指向移除节点的指针就会重新指向更新后的节点
  return node;
}

移除一个节点时，我们首先需要检测当前的节点是否为 null，如果是，说明要移除的键不在树中，我们直接返回 null。

如果当前检测的节点不为 null，我们继续在树中查找要移除的键。如果要找的键比当前节点的值小，说明要移除的键在树的左边，就沿着树的左边继续找下一个节点。如果要找的键比当前节点的值大，说明要移除的键在树的右边，那么就沿着树的右边继续找下一个节点。

如果找到了要找的键（键和 node.key）相等，需要处理三种不同的情况。

1、移除一个叶节点
第一种情况是要移除的节点是一个没有左侧子节点和右侧子节点的叶节点。在这种情况下，我们要做的就是给这个叶节点赋值 null 来移除它。在这里，这个叶节点没有任何子节点，但是它有一个父节点，因此需要通过返回 null 来将对应的父节点指向该叶节点的指针赋予 null 值。

如下图，展示了移除一个叶节点的过程：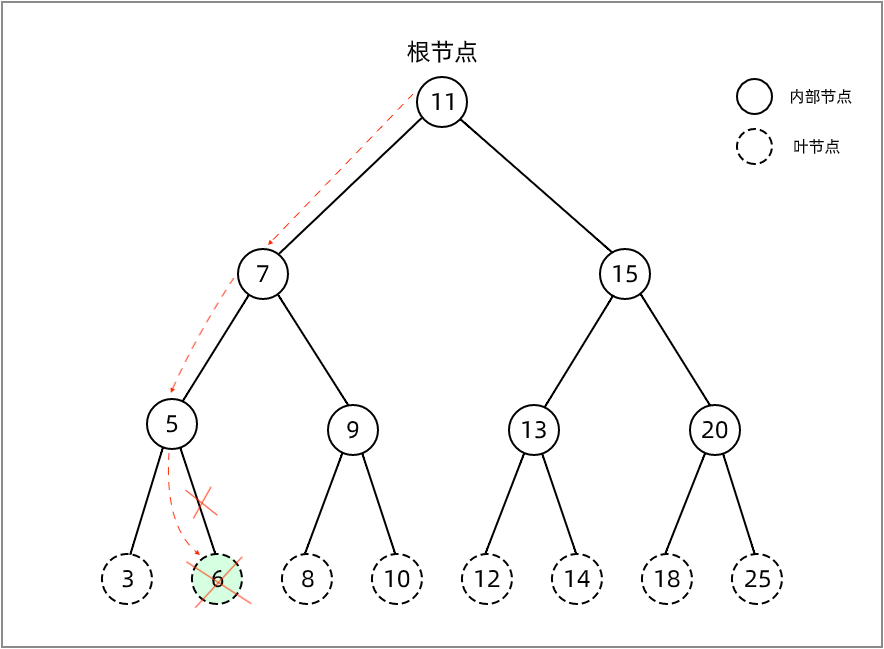

2、移除一个有左侧子节点或右侧子节点的节点
第二种情况是移除一个有左侧子节点或右侧子节点的节点。这种情况下，直接跳过这个要删除的节点，然后直接将它的父节点指向它的子节点。

如果这个节点没有左侧子节点，也就是说它只有右侧子节点。我们要做的事情就是把对它的引用改为对它的右侧子节点的引用，并返回更新后的节点。

如果这个节点没有右侧子节点，也就是说它只有左侧子节点，我们要做的事情就是把对它的引用改为它的左侧子节点的引用，并返回更新后节点。

如下图，展示了移除只有一个左侧子节点或右侧子节点的过程：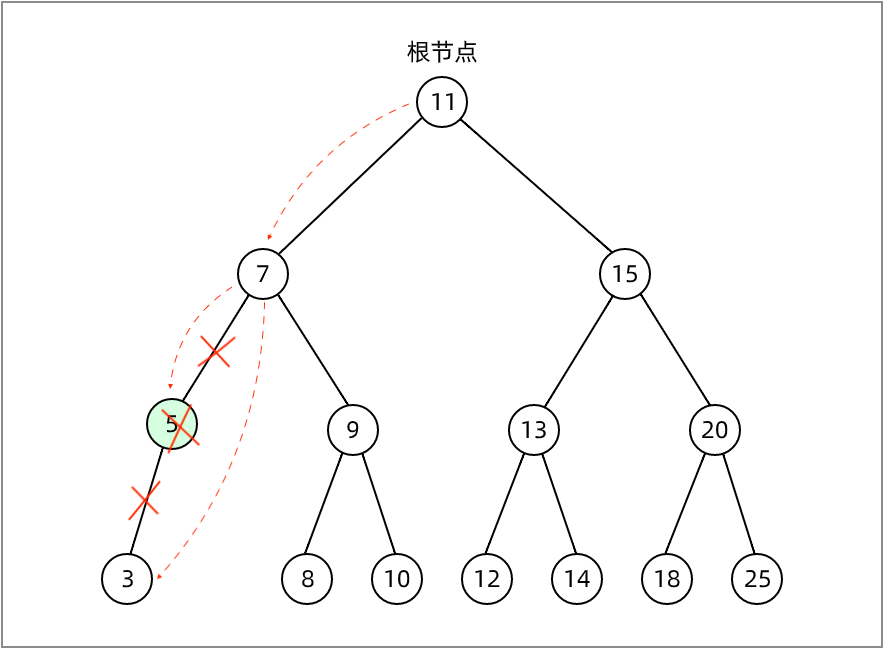


3、移除有两个子节点的节点**
要移除有两个子节点的节点，需要执行四个步骤：

(1) 当找到了要移除的节点后，需要找到它右边子树中最小的节点，如下图要删除的节点时15，它的右子树中最小节点是18。

(2) 然后，用右侧子树中国最小的节点的键去更新删除节点的值。通过这一步，我们改变了这个节点的键，也就是说它被移除了。在下图中，用节点15的右侧子树最小节点18去更新节点15的值。

(3)但是，这样在树中就有两个相同键的节点了，这是不行的。要继续把右侧子树中的最小节点移除，毕竟它已经被移至要删除的节点的位置了。

(4) 最后，向移除节点的父节点返回更新后节点的引用。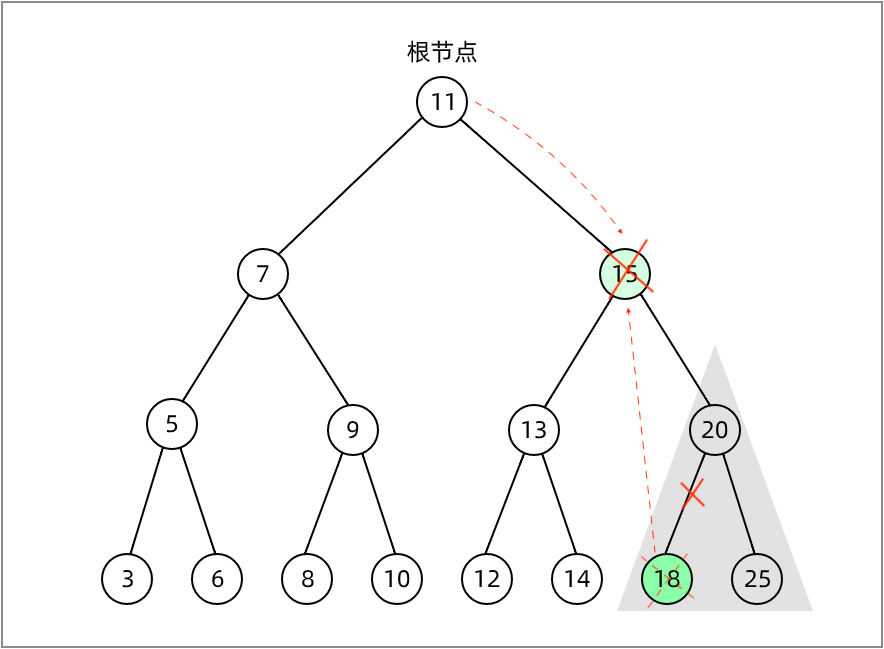

preOrderTraverse() 通过先序遍历方式遍历所有节点

先序遍历就是从根节点开始，然后递归遍历左子树，再递归遍历右子树，概括起来就是 根节点 -> 左子树 -> 右子树 。在每一棵子树的内部，都是重复这个顺序。先序遍历的一种应用就是打印一个结构化的文档。

preOrderTraverse(callback) {
    this.preOrderTraverseNode(this.root, callback);
}

preOrderTraverse 方法接收一个回调函数作为参数。回调函数用来定义我们对遍历到的每个节点进行的操作。在 preOrderTraverse 中使用了一个辅助方法，来接收一个节点和对应的回调函数作为参数。

preOrderTraverseNode(node, callback) {
  // 先序遍历的执行顺序：根节点 -> 左子树 -> 右子树
  if (node != null) {
    // 首先对根节点执行callback操作
    callback(node.key);
    // 然后递归遍历左子树
    this.preOrderTraverseNode(node.left, callback);
    // 最后再递归遍历右子树
    this.preOrderTraverseNode(node.right, callback);
  }
}

在辅助方法 preOrderTraverseNode 中，首先检查传入的node节点是否为null，如果为null，则会停止递归。

先序遍历的遍历顺序就是根节点 -> 左子树 -> 右子树，因此，我们首先对根节点进行callback 操作，然后递归遍历左子树，最后再递归遍历右子树。

下面描绘了 preOrderTraverse 方法的访问路径：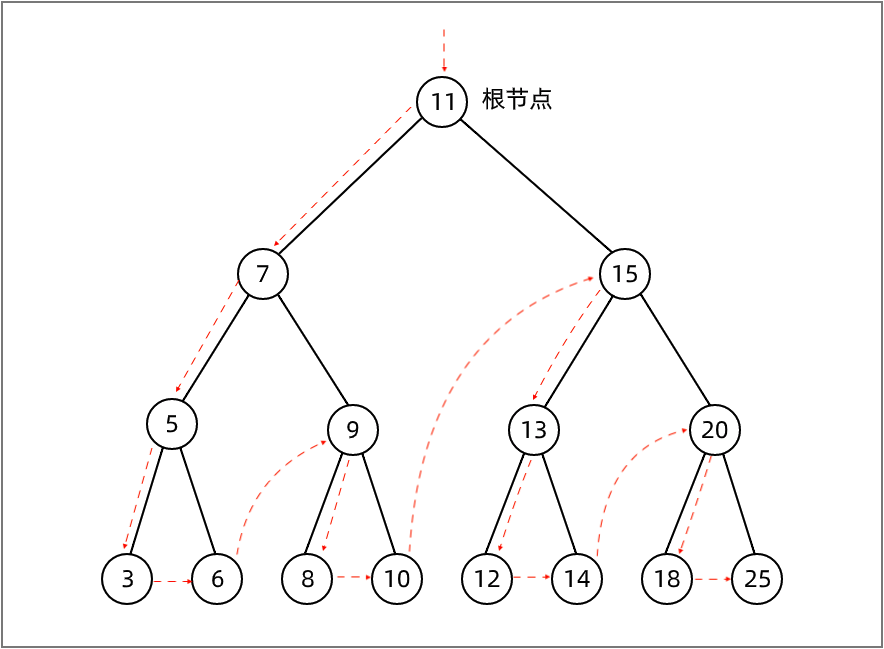

inOrderTraverse() 通过中序遍历方式遍历所有节点

中序遍历就是以从小到大的顺序访问所有的节点，其遍历顺序就是 左子树 -> 根节点 -> 右子树。中序遍历的一种应用就是对树进行排序。

inOrderTraverse(callback) {
    this.inOrderTraverseNode(this.root, callback)
}

inOrderTraverse 方法接收一个回调函数作为参数。回调函数用来定义我们对遍历到的每个节点进行的操作。在 inOrderTraverse 中使用了一个辅助方法，来接收一个节点和对应的回调函数作为参数。

inOrderTraverseNode(node, callback) {
  // 遍历顺序：左子树 -> 根节点 -> 右子树
    if (node != null) {
    // 递归边左子树
      this.inOrderTraverseNode(node.left, callback);
    // 对根节点进行 callback 操作
    callback(node.key);
    // 递归遍历右子树
    this.inOrderTraverseNode(node.right, callback);
  }
}

在辅助方法 inOrderTraverseNode 中，首先检查传入的node节点是否为null，如果为null，则会停止递归。

中序遍历的遍历顺序就是 左子树 -> 根节点 -> 右子树，因此，我们首先以递归的方式遍历左子树，遍历完左子树，对根节点进行一些操作(callback(node.key))，然后再对右子树递归遍历所有节点。

如下图描绘了 inOrderTraverse 方法的访问路径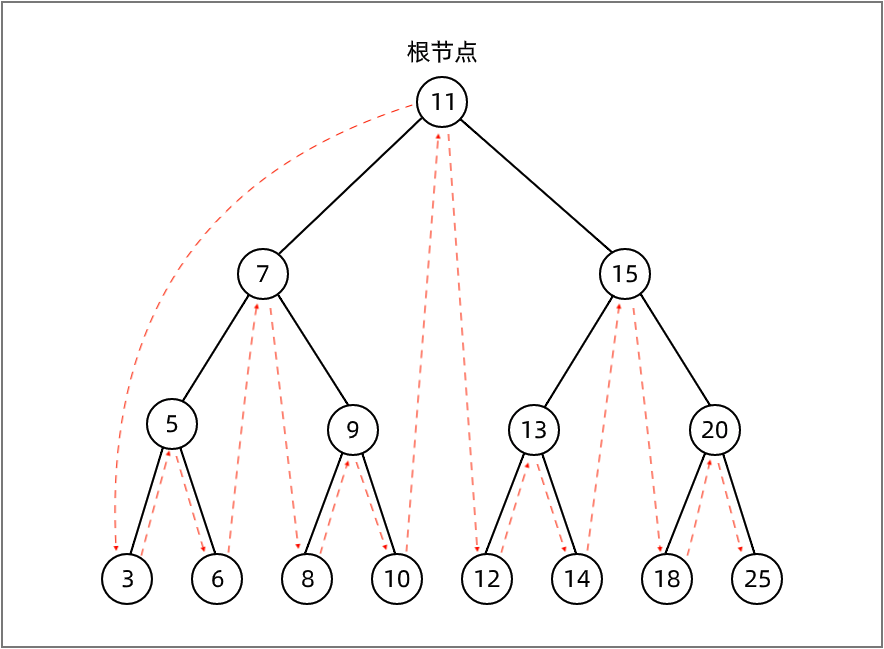

postOrderTraverse() 通过后序遍历方式遍历所有节点

后序遍历是先访问节点的后代节点，然后再访问节点本身。其遍历顺序是 左子树 -> 右子树 -> 根节点。后序遍历的一种应用是计算一个目录及子目录中所有文件所占空间的大小。

postOrderTraverse(callback) {
    this.postOrderTraverseNode(this.root, callback);
}

postOrderTraverse 方法接收一个回调函数作为参数。回调函数用来定义我们对遍历到的每个节点进行的操作。在 postOrderTraverse 中使用了一个辅助方法，来接收一个节点和对应的回调函数作为参数。

postOrderTraverseNode(node, callback) {
  // 遍历顺序是 左子树 -> 右子树 -> 根节点
    if (node != null) {
    // 递归左子树
      this.postOrderTraverseNode(node.left, callback);
    // 递归右子树
    this.postOrderTraverseNode(node.right, callback);
    // 对根节点进行 callback 操作
    callback(node.key);
  }
}

在辅助方法 postOrderTraverseNode 中，首先检查传入的node节点是否为null，如果为null，则会停止递归。

后序遍历的遍历顺序就是 左子树 -> 右子树 -> 根节点，因此，我们首先以递归的方式遍历左子树，遍历完左子树，然后再对右子树递归遍历所有节点，最后再对根节点进行callback操作(callback(node.key))。

下图描绘了 postOrderTraverse 方法的访问路径：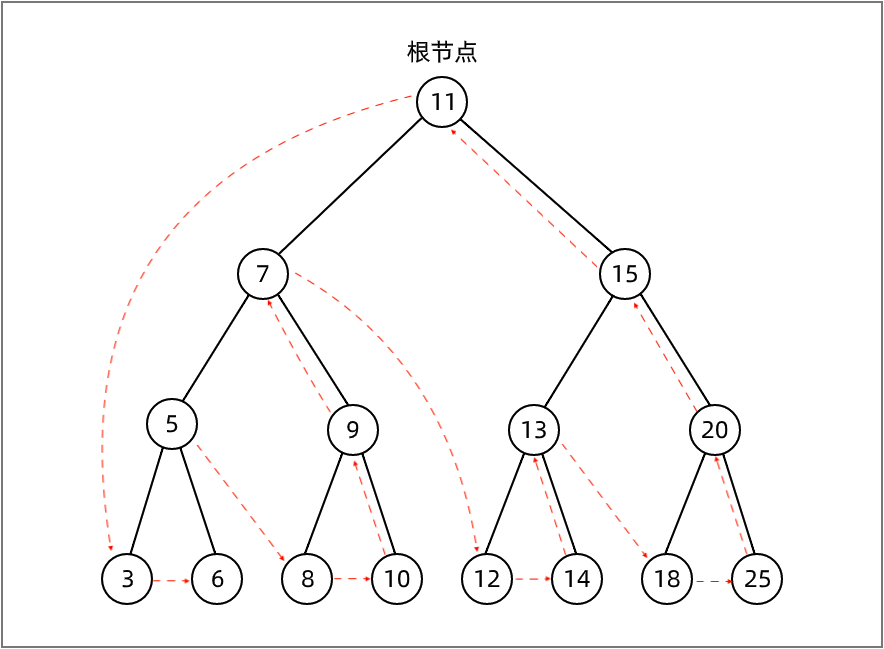

在先序遍历、中序遍历、后序遍历这三种遍历中，根节点的遍历分别被安排在了首要位置，中间位置和最后位置。所谓的 “先序”、“中序”和“后序”，“先”、“中”、“后”其实就是指根节点的遍历时机。

完整代码

import { Compare, defaultCompare } from '..util';
import { Node } from './models/node';
export default class BinarySearchTree {
    constructor(compareFn = defaultCompare) {
      this.compareFn = compareFn; // 用来比较节点值
    this.root = undefined; // 根节点
  }
  // 向树中插入一个节点
  insert(key) {
    if (this.root == null) {
      // 插入的是根节点
      this.root = new Node(key);
    } else {
      // 将节点添加到根节点以外的其它位置
      this.insertNode(this.root, key);
    }
  }
  insertNode(node, key) {
    // 要插入的节点的键小于父节点，则要插入的位置是左侧子节点
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      // 父节点没有左侧子节点，则在父节点的左侧子节点位置插入新节点
      if (node.left == null) {
        node.left = new Node(key);
      } else {
        // 父节点已有左侧子节点，则继续找到树的下一层，直到找到一个没有左侧子节点的节点，然后将新节点插入到该节点的左侧子节点的位置
        this.insertNode(node.left, key);
      }
    } else {
      // 要插入的节点的键大于父节点，则要插入的位置是右侧子节点
      if (node.right == null) {
        // 父节点没有右侧子节点，则在父节点右侧子节点的位置插入新节点
        node.right = new Node(key);
      } else {
        // 父节点已有右侧子节点，则继续找到树的下一层，直到找到一个没有右侧子节点的节点，然后将新节点插入到该节点的右侧子节点的位置
        this.insertNode(node.right, key);
      }
    }
  }
  // 获取根节点
  getRoot() {
    return this.root;
  }
  // 在树中查找一个键
  search(key) {
      return this.searchNode(this.root, key);
  }
  searchNode(node, key) {
      if (node == null) {
        return false;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
        return this.searchNode(node.left, key)
    } else if (this.compareFn(key, node.key) === Compare.BIGER_THAN) {
        return this.searchNode(node.right, key)
    }
    return true;
  }
  // 返回树中最小值
  min() {
      return this.minNode(this.root);
  }
  minNode(node) {
      let current = node;
    while(current != null && current.left != null) {
        current = current.left;
    }
    return current;
  }
  // 返回树中最大值
  max() {
      return this.maxNode(this.root);
  }
  maxNode(node) {
      let current = node;
    while(current != null && current.right != null) {
        current = current.right;
    }
    return current;
  }
  // 从树中移除一个值
  remove(key) {
      return this.removeNode(this.root, key);
  }
  removeNode(node, key) {
      if (node == null) {
        return false;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
        node.left = this.removeNode(node.left, key);
      return node;
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
        node.right = this.removeNode(node.right, key);
      return node;
    }
    if (node.left == null && node.right == null) {
        node = undefined;
      return node;
    }
    if (node.left == null) {
        node = node.right;
      return node;
    } else if (node.right = null) {
        node = node.left;
      return node;
    }
    const aux = this.minNode(node.right);
    node.key = aux.key;
    node.right = this.removeNode(node.right, aux.key);
    return node;
  }
  // 先序遍历的方式遍历所有节点
  preOrderTraverse(callback) {
      this.preOrderTraverseNode(this.root, callback);
  }
  preOrderTraverseNode(node, callback) {
      if (node != null) {
        callback(node.key);
      this.preOrderTraverseNode(node.left, callback);
      this.preOrderTraverseNode(node.right, callback);
    }
  }
  // 中序遍历的方式遍历所有节点
  inOrderTraverse(callback) {
      return this.inOrderTraverseNode(this.root, callback);
  }
  inOrderTraverseNode(node, callback) {
      if (node != null) {
        this.inOrderTraverseNode(node.left, callback);
      callback(node.key);
      this.inOrderTraverseNode(node.right, callback);
    }
  }
  // 后序遍历的方式遍历所有节点
  postOrderTraverse(callback) {
      return this.postOrderTraverNode(this.root, callback);
  }
  postOrderTraverseNode(node, callback) {
      if (node != null) {
        this.postOrderTraverseNode(node.left, callback);
      this.postOrderTraverseNode(node.right, callback);
      callback(node.key);
    }
  }
}