前序遍历构造二叉搜索树

题目

题目来源：力扣（LeetCode）

返回与给定前序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。

(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，前序遍历首先显示节点 node 的值，然后遍历 node.left，接着遍历 node.right。）

题目保证，对于给定的测试用例，总能找到满足要求的二叉搜索树。

示例：

输入：[8,5,1,7,10,12]
输出：[8,5,10,1,7,null,12]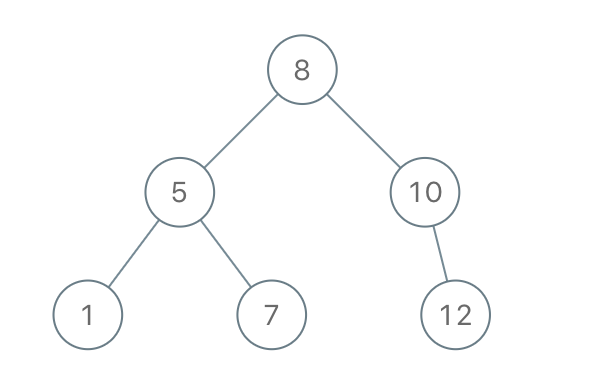

思路分析

二分查找左右子树的分界线递归构建左右子树

二叉搜索树的前序遍历顺序是：根节点 -> 左子树 -> 右子树，因此对于前序序遍历的结果数组，数组的第一个元素一定是二叉树搜索树的根节点。

又根据二叉搜索树的性质，左子树的所有节点值均小于根节点值，右子树上的所有节点均大于根节点，因此，我们可以把前序遍历的结果数组除了第一个元素以外后面的部分，分成两个区间：

• 第 1 个区间的所有元素都严格小于根节点，我们可以递归构建成根节点的左子树
• 第 2 个区间的所有元素都严格大于根节点，我们可以递归构建成根节点的右子树

我们可以使用二分法找到这两个区间的分界线，我们通过题目中的例子具体说明。

对于数组 [8, 5, 1, 7, 10, 12]，8 是二叉搜索树的根节点，5、1、7 都比 8 小，所以它们都是8的左子节点，10、12都比8大，所以它们都是 8 的右子节点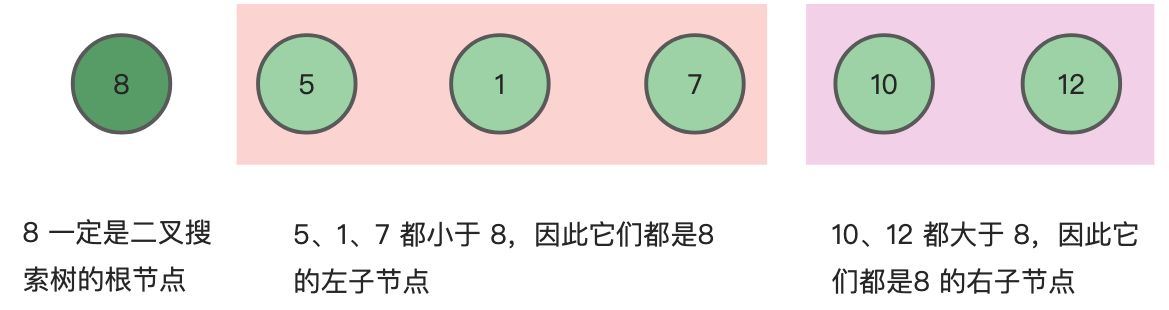

我们继续对子区间 [5, 1, 7] 进行二分拆分，5 是根节点，1 比 5 小，因此它是 5 的左子节点，7 比 5 大，因此它是 5 的右子节点。同理，子区间 [10, 12] 中 10 是根节点，比 10 大的 12 是 右子节点。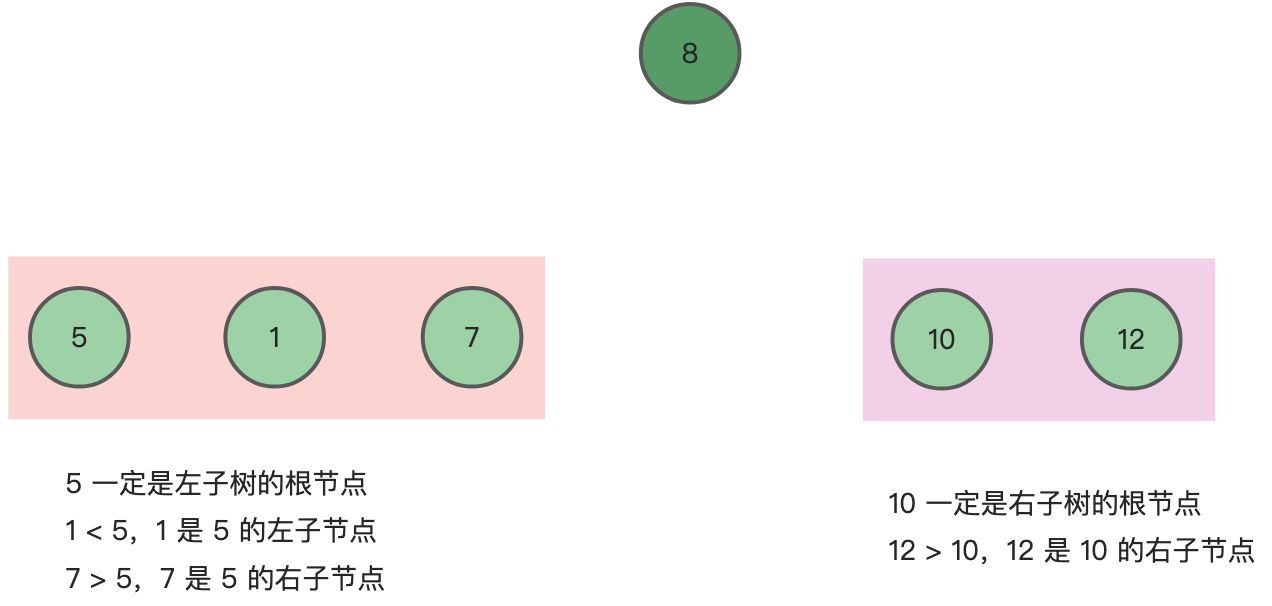

我们一直这样通过二分法拆分下去，直到不能拆分为止，最终得到如下的一棵二叉搜索树：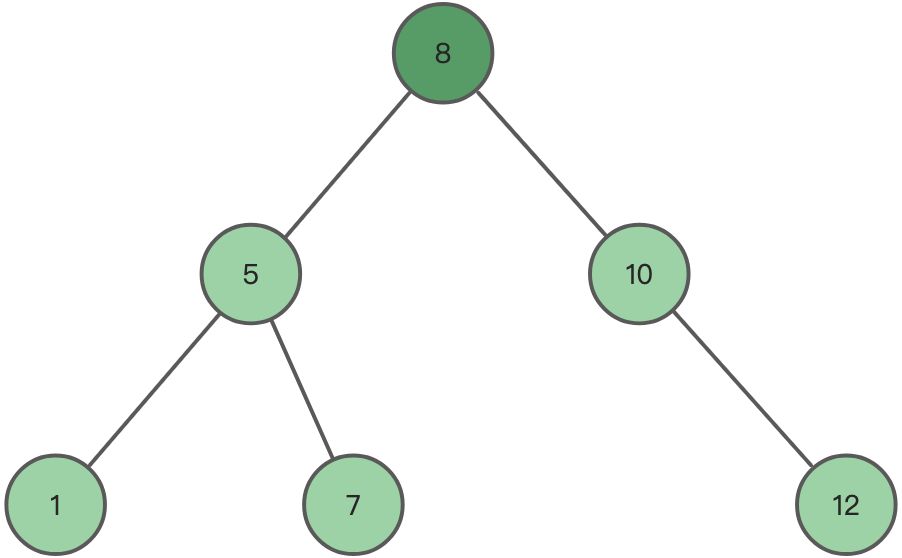

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
// 前序遍历的结果数组的范围是 left (数组的第一个元素的下标) 到 right (数组的最后一个元素的下标)
var buildTree = function (nums, left, right) {
  if (left > right) return null;
  // 前序遍历的结果数组的第一个元素一定是根节点
  // 因此从第二个元素开始到最后一个元素，查找左右子树的分界线
  let ind = left + 1; 
  // 拆分成两个区间，第一个区间 [left + 1, ind] 的元素都是比根节点 nums[left] 小的
  // 第二个区间 [ind + 1, right] 的元素都是比根节点 nums[left] 大的
  while (ind <= right && nums[ind] < nums[left]) ++ind;
  //构造根节点
  let root = new TreeNode(nums[left]);
  // 区间 [left + 1, ind] 的所有元素都是 root 节点的左子节点
  root.left = buildTree(nums, left + 1, ind - 1);
  // 区间 [ind + 1, right] 的所有元素都是 root 节点的右子节点
  root.right = buildTree(nums, ind, right);
  return root;
};
var bstFromPreorder = function (preorder) {
  // 传入前序遍历的结果数组、数组的第一个元素的下标、数组最后一个元素的下标
  return buildTree(preorder, 0, preorder.length - 1);
};

直接插入

二叉搜索树的前序遍历顺序是：根节点 -> 左子树 -> 右子树 。
二叉搜索树的性质是：

• 左子树上所有节点的值均小于它的根节点的值；
• 右子树上所有子节点的值均大于它的根节点的值；

我们可以根据上面的两个性质，直接将节点插入树中。例如我们在下面的二叉搜索树中插入节点 7：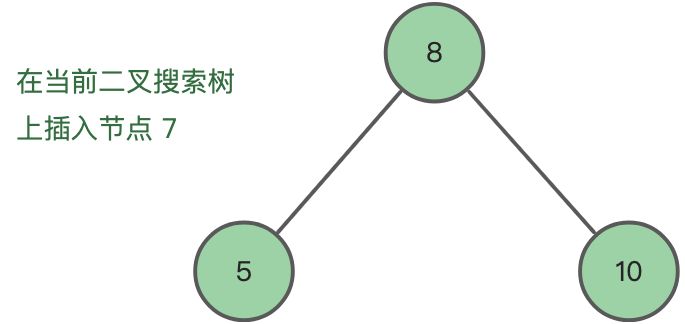

第一步，节点 7 与 根节点 8 比较，7 小于 8，因此节点 7 应该插入到 8 的左子树上：

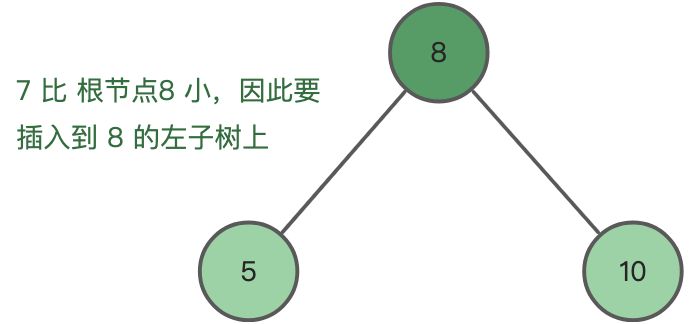
第二步，节点7 与 根节点8 的左子节点5 比较，7 大于 5，因此节点7 应该插入到节点5 的右子树上：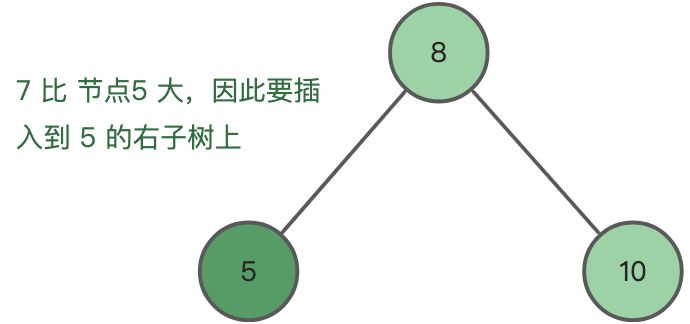

第三步，由于节点5的右子树是空的，因此直接将节点7作为节点5的右子树， 插入到节点5的右子节点上即可：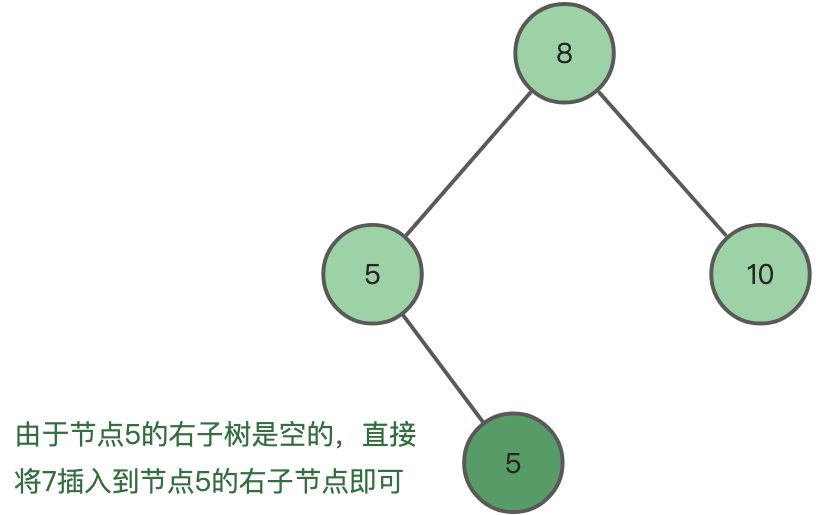

往树中插入一个节点的代码如下：

// data 是要插入的节点值
const addTreeNode = (root, data) => {
  // 新建一个节点
  const node = new TreeNode(data);
  let p = root;
  while (true) {
    // 如果要插入的节点值data 比节点p 的值小，则将要插入节点插入点节点p 的左子树上
    if (p.val > data) {
      // 如果节点p 的左子节点为空，直接作为节点p的左子节点
      if (p.left == null) {
        p.left = node;
        break;
      } else {
        p = p.left
      }
    } 
    // 如果要插入的节点值data 比节点p 的值大，则将要插入节点插入点节点p 的右子树上
    else {
      // 如果节点p 的右子节点为空，直接作为节点p的右子节点
      if (p.right == null) {
        p.right = node;
        break;
      } else {
        p = p.right;
      }
    }
  }
}

那么要构建一棵二叉搜索树，我们只需要依次数组中的元素，然后将元素一一插入到树中即可，代码如下：

var bstFromPreorder = function (preorder) {
  const root = new TreeNode();
  root.val = preorder[0];
  // 遍历数组，将元素值添加到树上
  for (let i = 1; i < preorder.length; i++) {
    addTreeNode(root, preorder[i])
  }
  return root
}

完整代码：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
// data 是要插入的节点值
const addTreeNode = (root, data) => {
  // 新建一个节点
  const node = new TreeNode(data);
  let p = root;
  while (true) {
    // 如果要插入的节点值data 比节点p 的值小，则将要插入节点插入点节点p 的左子树上
    if (p.val > data) {
      // 如果节点p 的左子节点为空，直接作为节点p的左子节点
      if (p.left == null) {
        p.left = node;
        break;
      } else {
        p = p.left
      }
    } 
    // 如果要插入的节点值data 比节点p 的值大，则将要插入节点插入点节点p 的右子树上
    else {
      // 如果节点p 的右子节点为空，直接作为节点p的右子节点
      if (p.right == null) {
        p.right = node;
        break;
      } else {
        p = p.right;
      }
    }
  }
}
var bstFromPreorder = function (preorder) {
  const root = new TreeNode();
  root.val = preorder[0];
  // 遍历数组，将元素值添加到树上
  for (let i = 1; i < preorder.length; i++) {
    addTreeNode(root, preorder[i])
  }
  return root
}

递归构建

原理与上面的直接插入方式相同，只是上面的方法中插入节点的时候使用的是 while 循环，代码量较多，我们可以改成递归的方式：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
const addTreeNode = (root, val) => {
  if (root == null)
    return new TreeNode(val);
  // 如果要插入的节点值data 比节点p 的值小，则将要插入节点插入点节点p 的左子树上
  else if (root.val > val) 
    root.left = addTreeNode(root.left, val);
  // 如果要插入的节点值data 比节点p 的值大，则将要插入节点插入点节点p 的右子树上
  else
    root.right = addTreeNode(root.right, val);
  return root;
}
var bstFromPreorder = function (preorder) {
  const root = new TreeNode();
  root.val = preorder[0];
  // 遍历数组，将元素值添加到树上
  for (let i = 1; i < preorder.length; i++) {
    addTreeNode(root, preorder[i])
  }
  return root
}

借助单调栈构建

我们使用一个栈来维护二叉搜索树中的节点，栈中存放的是已经构建好的二叉搜索树的节点 (但不是全部，有些已经可能出栈了)，其中栈中元素从栈底掉栈顶是单调递减的。

算法

1. 首先将先序遍历的结果数组的第一个元素作为二叉搜索树的根节点，即 root = new TreeNode(preorder[0])，并将其放入栈中。
2. 使用for循环遍历先序遍历的结果数组中剩下的元素，将栈顶的元素作为父节点，当前遍历的元素作为子节点：
   1. 如果当前遍历的元素的值 小于 栈顶元素的值，我们直接让当前元素作为栈顶元素节点的左子节点，然后将当前元素入栈
   2. 如果当前遍历的元素的值 大于 栈顶元素的值，我们就让栈顶元素出栈，直到当前元素的值 小于 栈顶元素的值或栈为空为止。此时最后一个被弹出栈的元素节点就是当前遍历元素的父节点，而当前元素是它父节点的右子节点。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
let bstFromPreorder = (preorder) => {
  //生成根节点并将其推入栈中
  let root = new TreeNode(preorder[0]);
  // 栈中存放的是已经构建好的二叉搜索树的结点（但不是全部，有些可能已经出栈了）
  // 其中栈中元素从栈底到栈顶是递减的
  let stack = [root];
  //遍历preorder插入节点
  for (let i = 1; i < preorder.length; i++) {
    // 创建节点
    let currentNode = new TreeNode(preorder[i]);
    // 栈顶元素
    let node = stack[stack.length - 1];
    // 如果当前遍历的元素的值 大于 栈顶元素的值，
    // 我们就让栈顶元素出栈，直到当前元素的值 小于 栈顶元素的值或栈为空为止。
    // 此时最后一个被弹出栈的元素节点就是当前遍历元素的父节点，而当前元素是它父节点的右子节点
    if (currentNode.val > node.val) {
      //把栈中小于当前节点的值全部弹出
      while (stack.length && stack[stack.length - 1].val < currentNode.val) {
        node = stack.pop();
      }
      // 此时的node指向栈最后一个弹出的节点
      node.right = currentNode;
    }
    // 如果当前遍历的元素的值 小于 栈顶元素的值，我们直接让当前元素作为栈顶元素节点的左子节点，
    // 然后将当前元素入栈
    else {
      // 此时的node指向栈中的最后一个节点
      node.left = currentNode;
    }
    stack.push(currentNode);
    // 当前节点当作下一个父节点
  };
  return root;
};

参考： https://leetcode-cn.com/problems/construct-binary-search-tree-from-preorder-traversal/solution/javadai-ma-de-5chong-jie-ti-si-lu-by-sdwwld/ https://leetcode-cn.com/problems/construct-binary-search-tree-from-preorder-traversal/solution/jian-kong-er-cha-shu-by-leetcode/