单调栈 - 柱状图中最大的矩形 - 《数据结构与算法》

题目
思路分析

题目

题目来源：力扣（LeetCode）

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

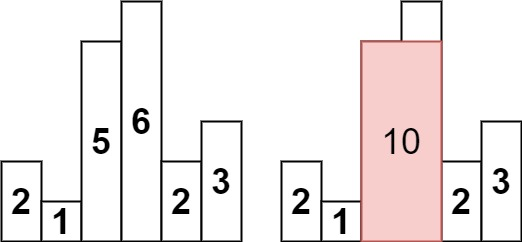
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

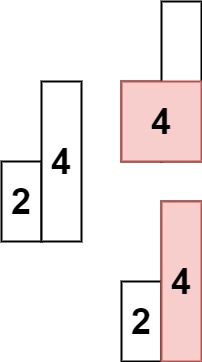
输入： heights = [2,4]
输出： 4

思路分析

先将题目给定的数组左右各添加一个元素0，为了方便确定原有数组中第一个元素和最后一个元素能不能继续扩张；
然后开始从左到右依次遍历数组中的元素：
1. 如果栈为空或者当前考察的新元素值比栈顶元素值大，表明以栈顶元素值为高的矩形面积暂不能确定，所以就将当前考察的新元素入栈。在这个条件下，栈中的元素值从栈底到栈顶是依次递增的；
2. 如果栈不为空且当前考察的新元素值比栈顶元素值小，表明以栈顶元素值为高的矩形的面积是可以确定的了。(在确定一个柱形的面积的时候，除了右边要比当前严格小，其实还蕴含了一个条件，那就是左边也要比当前高度严格小) 该矩形的高就是栈顶元素值，其右侧边界就是当前考察的新元素，左侧边界是栈顶元素的前一个元素，因为，在上一步中我们知道栈中元素值从栈底到栈顶是依次递增的。因此，矩形的宽是当前考察的元素索引与栈顶元素前一个元素的索引的差值减一。

这里需要注意的是，当栈顶元素出栈后，需要继续看当前考察的新元素值是否小于新的栈顶元素值，如果是，就继续将栈顶元素弹出，然后计算以其值为高的矩形面积，直到当前考察的新元素值大于栈顶元素值时，当前考察元素入栈。

最后，由于最终计算矩形面积时，是用两个柱子的索引来确定矩形宽度的。因此，栈中存储的应该是给定数组的索引。

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
  // 初始化最终结果为 0
  let res = 0;
  // 维护一个单调递增的栈，栈中存储的是索引值，
  // 从栈底到栈顶，索引值严格单调递增，同时对应的高度值也严格单调递增
  const stack = [];
  // 将题目给定的数组左右各添加一个元素0，为了方便确定原有数组中第一个元素和最后一个元素能不能继续扩张
  const newHeights = [0, ...heights, 0];
  for (let i = 0; i < newHeights.length; i++) {
    // 如果栈不为空且当前考察的元素值 小于 栈顶元素值，
    // 那么以栈顶元素值为高的矩形面积是可以确定的，弹出栈顶元素，并计算面积
    while (stack.length && newHeights[i] < newHeights[stack[stack.length - 1]]) {
      // 弹出栈顶元素
      const curIndex = stack.pop();
      // 获取栈顶元素对应的高
      const curHeight = newHeights[curIndex];
      // 栈顶元素弹出后，新的栈顶元素就是其左侧边界
      const leftIndex = stack[stack.length - 1];
      // 右侧边界是当前考察的索引
      const rightIndex = i;
      // 计算矩形的宽度，两边都不算，只算左边界和右边界中间的距离，所以减 1
      const curWidth = rightIndex - leftIndex - 1;
      // 计算面积
      res = Math.max(res, curWidth * curHeight);
    }
    // 当前考察的索引入栈
    stack.push(i);
  }
  return res;
}

借鉴：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/dong-hua-yan-shi-dan-diao-zhan-84zhu-zhu-03w3/