Bag of words
You may notice that we did not care about the ordering of tokens in document → Bag-of-Words (Bow) assumption 你会发现我们只关心文档中编译的词,而不在乎他们的顺序。
• A document is a collection of words
– Doc1: The cat ate the fish
– Doc2: The fish ate the cat
– These two documents are the same under BoW assumption 在bow假设下,以上句话是相同的
• We will use the BoW assumption throughout the IR part of the course 这门课在IR部分使用bow假设
• Real world systems (e.g. google) do have to consider ordering 但是实际世界会考虑顺序问题
• The NLP section will cover approaches that consider ordering NLP部分会考虑语序
Boolean retrieval
- bag of words & documents fields
Field (Zone) in Document
A partial solution to the weakness of BoW Bow有一个弱点
• Documents may be semi-structured: 文章可能都是相似结构的
– Title
– Author
– Published date
– Body – …
• Users may want to limit search scope to a certain field 用户可能想把搜索限制在某个特定的结构区域内
Basic Field Index
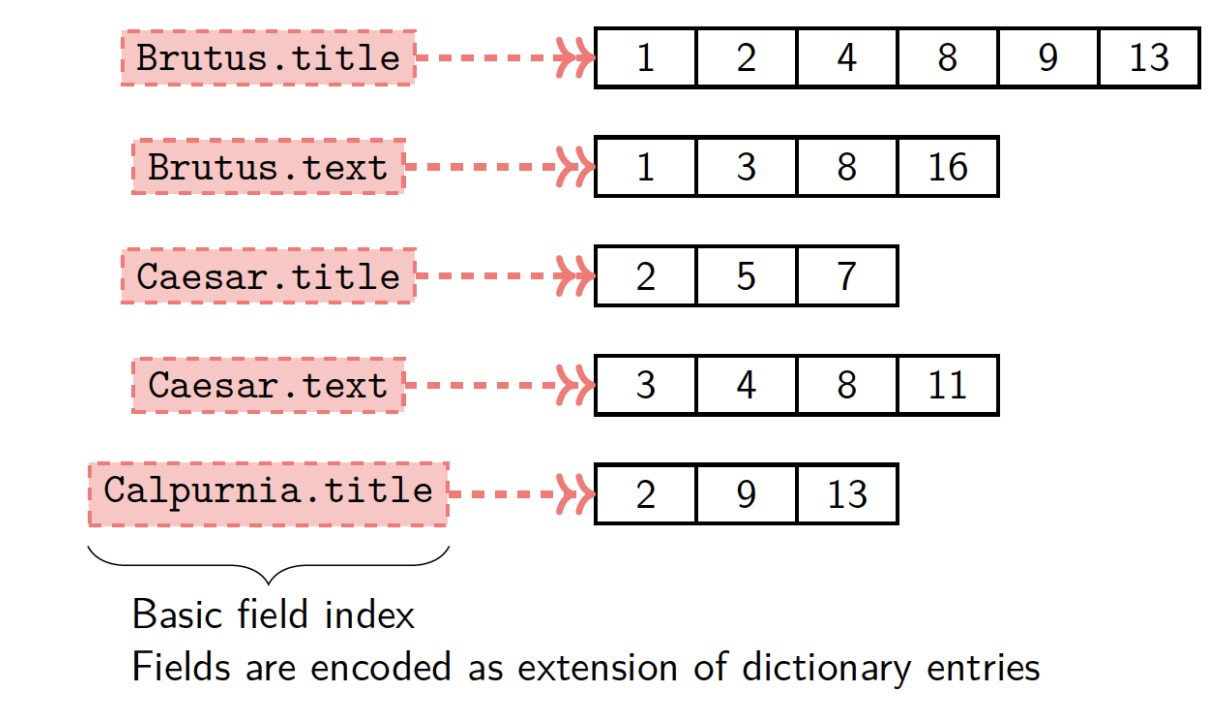
Equivalent to a separate index for each field. 相当于每个字段的单独索引
Field in Posting
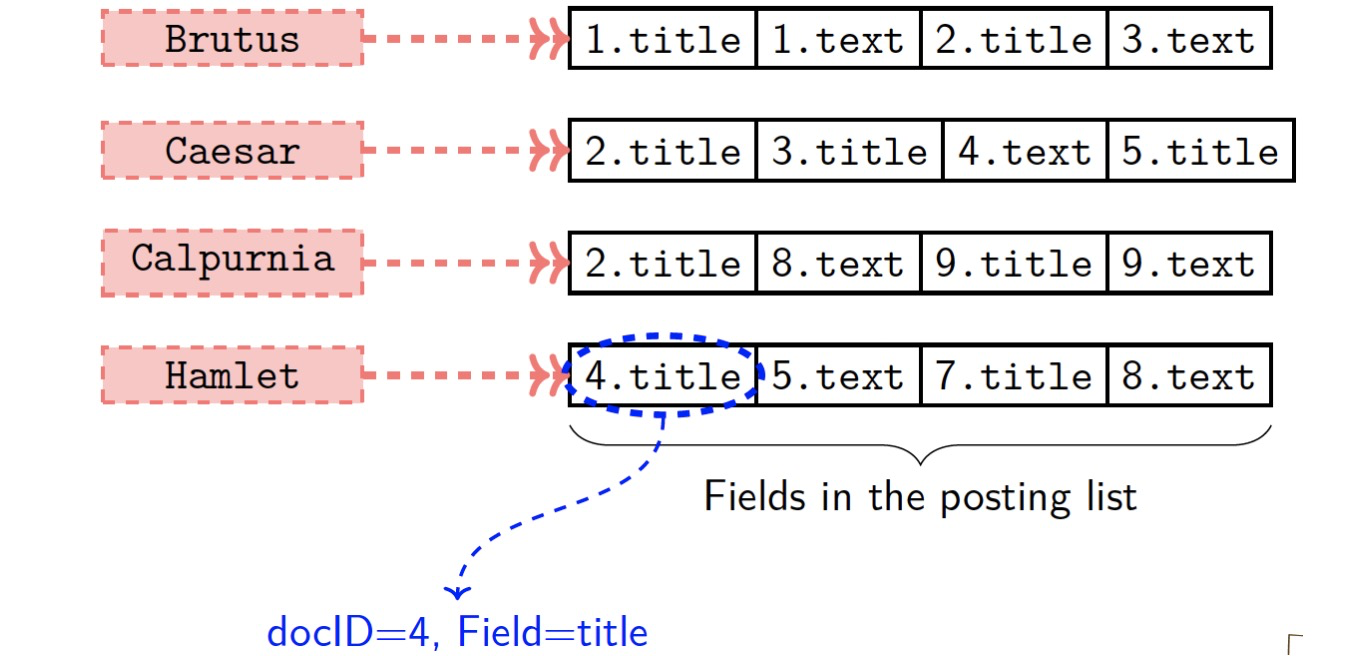
Reduces the size of the dictionary. Enables efficient weighted field scoring 减小了字典的大小
Boolean Retrieval with Field
Ranked retrieval
Limitations of Boolean Retrieval
Thus far, our queries have all been Boolean.
– Documents either match or don’t 文件匹配或者不匹配
• Good for expert users with precise understanding of their needs and the collection 适合专家用户,他们更理解自己的需求
• Not good for the majority of users 但不适合大多数用户
– Most users are incapable of writing Boolean queries
– Or they find it takes too much effort
• Boolean queries often result in either too few or too many results 可能会出现太多,或者太少的搜索结果
– Query1: “bluetooth pairing iphone” → 100,000 hits
– Query2: “bluetooth pairing iphone sony mdr-xb50” → 0 hits
Ranked Retrieval
Given a query, rank documents so that “best” results are early in the list. 给一个查询语句,最好的结果会排在更靠前的位置上
• When result are ranked a large result set is not an issue.
• We only show the top k(~10) results. 只展示 前k(~10)的结果
• We don’t overwhelm the user. Need a scoring function for document 𝑑 and query 𝑞:
𝑆𝑐𝑜𝑟𝑒(𝑑, 𝑞)
Documents with a larger score will be ranked before those with a smaller score. 比分更大的文档会出现在小比分文档之前
Weighted Fields Approach
Advanced search is for experts 为专家准备高级搜索
– most users use simple keyword queries 大多数用户使用简单关键词搜索
• How can we still make use of the fields without extra effort from the user? 我们怎样使用区域信息而不需要用户付出其他努力?
• Intuitively, term importance depends on location 将词汇的重要性与位置关联
– Terms in the headline of news article are typically more important than terms in main text.
例如:出现在新闻标题的词汇要比正文中出现的更重要
Scoring with Weighted Fields

gi是权重, 所有权重累加起来为1.
出现在某个区域,si为1,并乘以当前区域的权重。 如果没有出现,则si为0.
In short: If a query term occurs in field 𝑖 of a document then add 𝑔𝑖 to the score for that document and term

Rank by Term Frequency

定义:tf是某个词汇在文档中出现的次数
So far we ignored the frequency of term t in document d.
• We can rank based on the frequency of query terms in documents 我们可以基于词汇出现在文章中的频率来排序
• Let q be a set of query terms (w1 , w2 , …, wm), a term frequency score of documents given query q is: q 是查询语句中的词集合,文章的词频则是: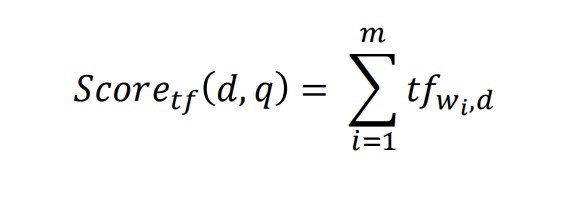
Example

Importance of Terms
Every term could have a different weight 每个词汇都应该有不同的权重
– A collection of documents on the auto industry is likely to have the term car in almost every document. 在汽车行业,几乎每篇文章都会出现‘汽车’
• How can we reduce the weight of terms that occur too often in the collection? 我们怎样衡量那些出现在文章中过于频繁的词汇?
– →Use the document frequency of the terms. 对词汇使用权重
document frequency
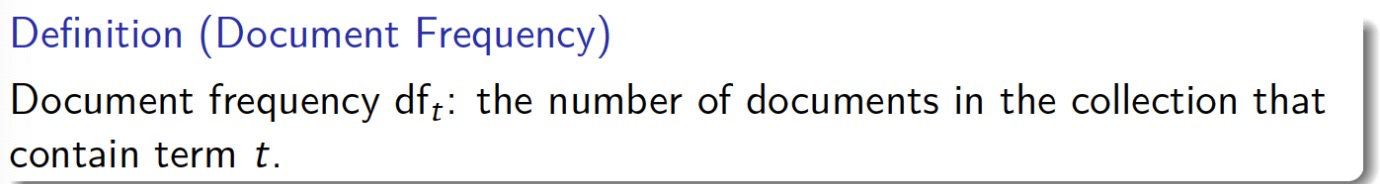
定义:文档频率 df 是包含词汇 t 的文档数量
df is a good way to measure an importance of a term.
– High frequency → not important (like stopwords) 频率越高,越不重要
– Low frequency → important 频率越低,越重要
Why not collection frequency? (The total number of occurrences of a term in the collection. Denoted cf) 为什么不用词汇的出现频率 cf 代替 df?
cf and df behave very differently in this example. cf is sensitive to documents that contain a word many times. 因为 cf 对同一个文章中多次出现某词汇敏感。
Inverse Document Frequency 反向文档频率

定义:df文档频率是包含词汇 t 的文档数量, N为文档总数量
The idf of a rare term is high, whereas the idf of a frequent term is likely to be low. 稀有词汇的idf会很高,而经常性出现的词汇则会很低
– E.g., Let N = 100, dfcar = 60, dfinsurance = 10
– idfcar = 0. 22, idfinsurance = 1 (using log base 10)
→ insurance is 4 times more important than car.
– Other log bases are sometimes such as log base e or log base 2.
TF-IDF

Using tf-idf weights, the score of document d given query q = (t1 , t2 , …, tm) is: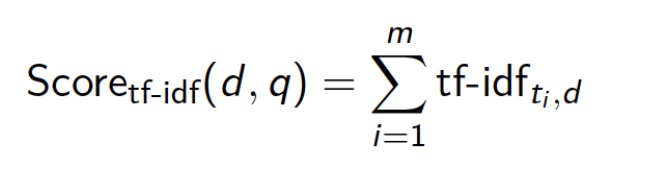
tf 词频率 * 反向文档频率
EXAMPLE
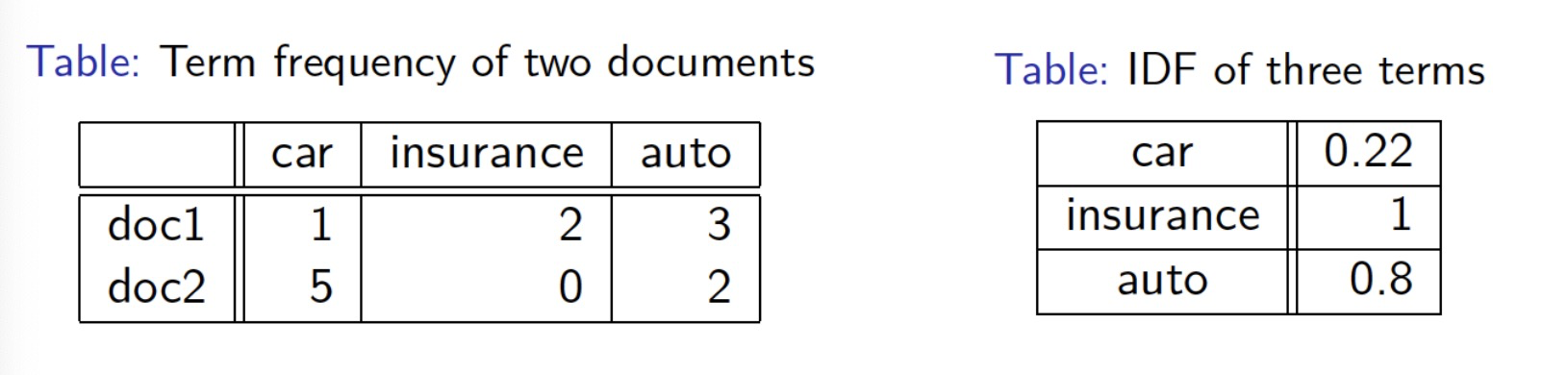
Given the query “car insurance”, the score of each document is:
– Score(doc1, q) = tf-idfcar,doc1 + tf-idfinsurance,doc1 = 2.22
– Score(doc2, q) = tf-idfcar,doc2 + tf-idfinsurance,doc2 = 1.1
• Unlike the tf scoring approach, the score of doc1 is greater than doc2.
Limitation of tf-idf scoring tf-idf的限制
tf-idf relies heavily on term frequency. tf-idf严重依赖术语频率。
Example:
– tfcar, doc1 = 20
– tfcar, doc2 = 1
– If our query contains “car”, then the tf-idfcar score of doc1 is 20
times larger than for doc2.
tf-idf score increases linearly with term frequency
Claim: the marginal gain of term frequency should decrease as term frequency increases.
- The relationship should be non-linear 应该是非线性关系
Sublinear tf scaling
- Use logarithmically weighted term frequency (wf) 使用对数函数来权重tf
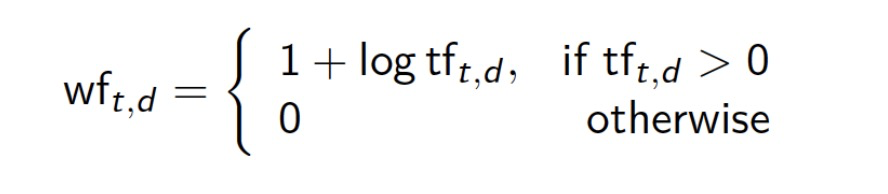
- Logarithmic term frequency version of tf-idf
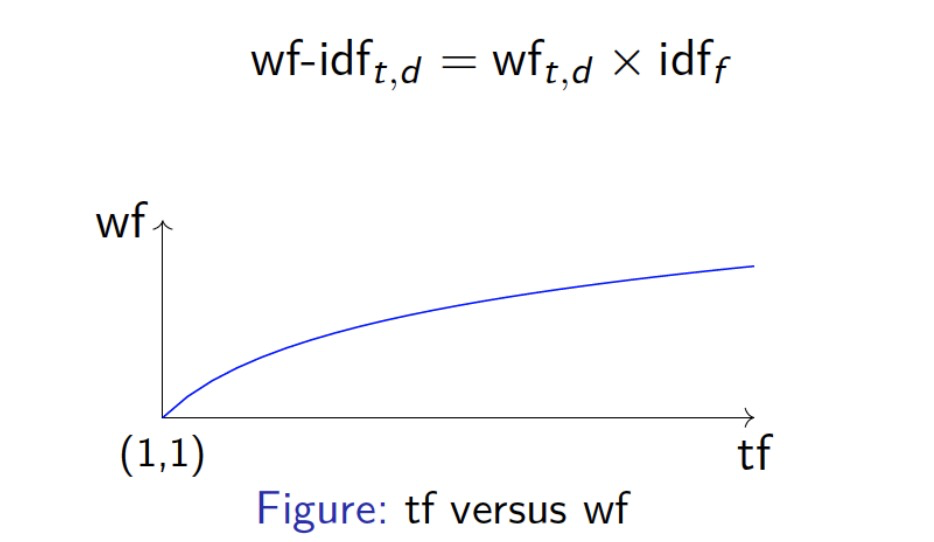
A limitation of tf-idf/wf-idf scoring
Assume we have document d 假设我们有一个文档d
• We create a new document d’ by appending a copy of d to itself (d’ = d X 2). 新建一个文档d‘ 是复制d两次
• While d’ should be no more relevant to any query than d, their scores are different! 尽管d‘没有和查询语句更相关,但是他们的分数是不同的。
– Scoretf-idf (d’, q) >= Scoretf-idf (d, q)
– Scorewf-idf (d’, q) >= Scorewf-idf (d, q)
– Both scoring methods prefer longer documents 分数算法更亲睐长文档
Maximum tf normalization
- Let tfmax(d) be the maximum frequency of any term in document d。 tfmax是文档d中的最大词频
- Normalized term frequency is defined as
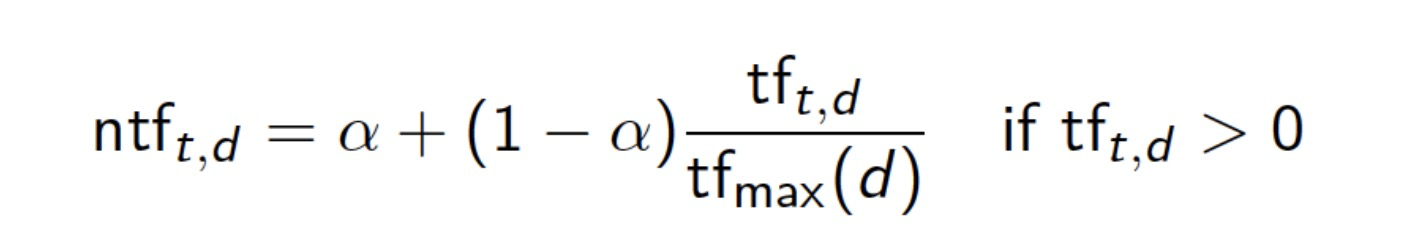
– Maximum value of ntf is 1
– Minimum value of ntf is α
This approach also has limitations. (can be skewed by a single term that occurs frequently) 也有缺陷,可能被频繁出现的单个术语扭曲
Document as Vectors
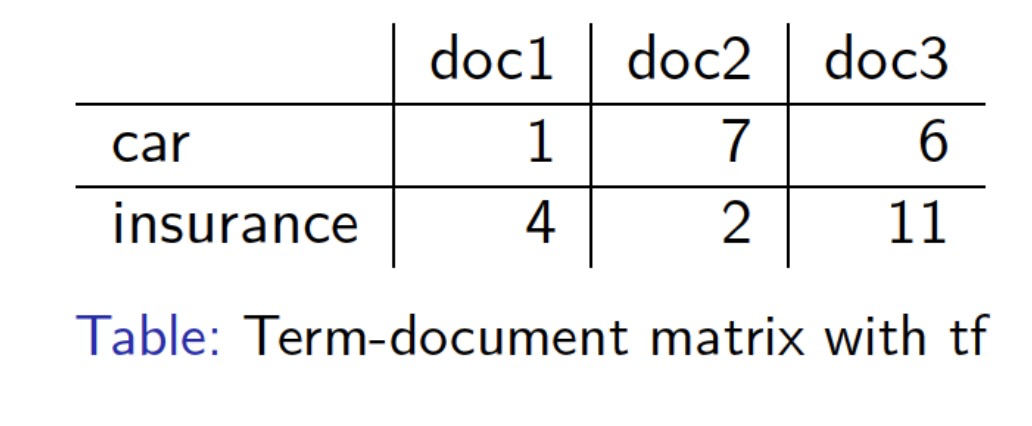
• Given a term-document matrix
– a document can be represented as a vector of length V 一个文档可以由长度为V的向量表示
– V = size of vocabulary 词汇表大小V
• Document vectors:
– d1 = (1, 4), d2 = (7, 2), d3 = (6, 11)
Document Similarity in Vector Space 在向量空间中文档的相似度
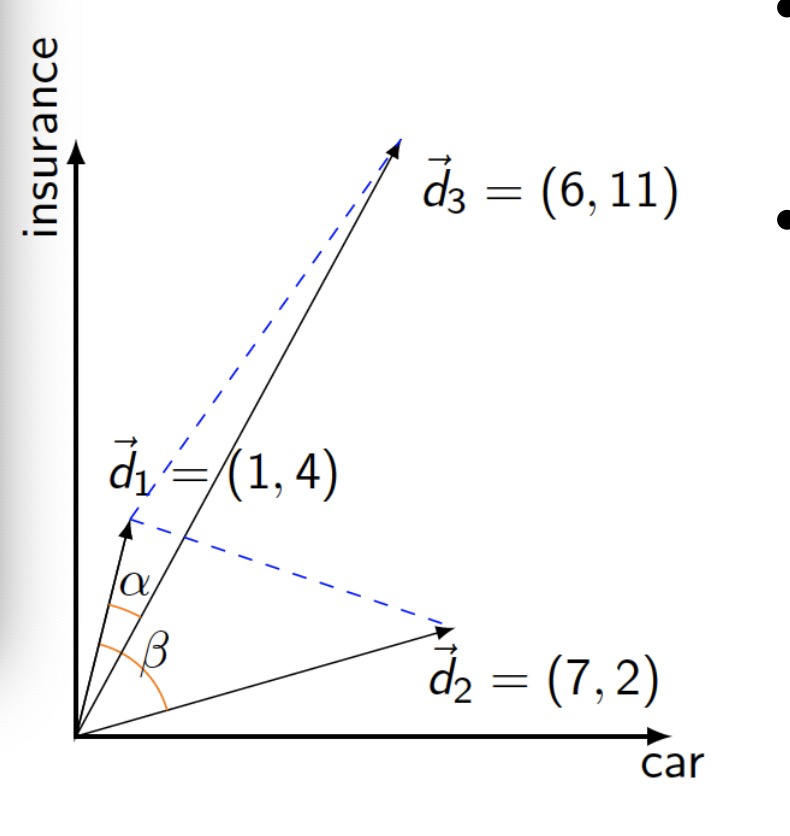
• Plot document vectors in vector space
• How to find similar documents in vector space?
– Distance from vector to vector 向量之间的距离
– Angle difference between vectors 向量之间的角度
Angle Difference 角度差
- Cosine similarity: 余弦相似度
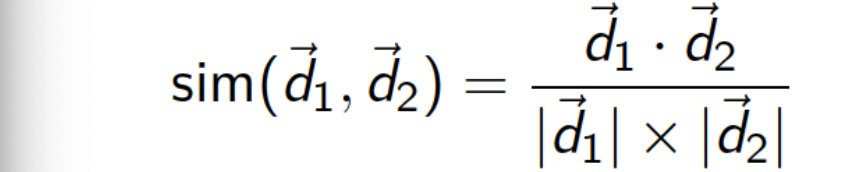
– Numerator: inner product 点积
– Denominator: product of Euclidean lengths
• Standard way of quantifying similarity between documents
– 1 if directions of two vectors are the same 两个向量完全相同则为1
– 0 if directions of two vectors are orthogonal (90) 两个向量是直角则为0
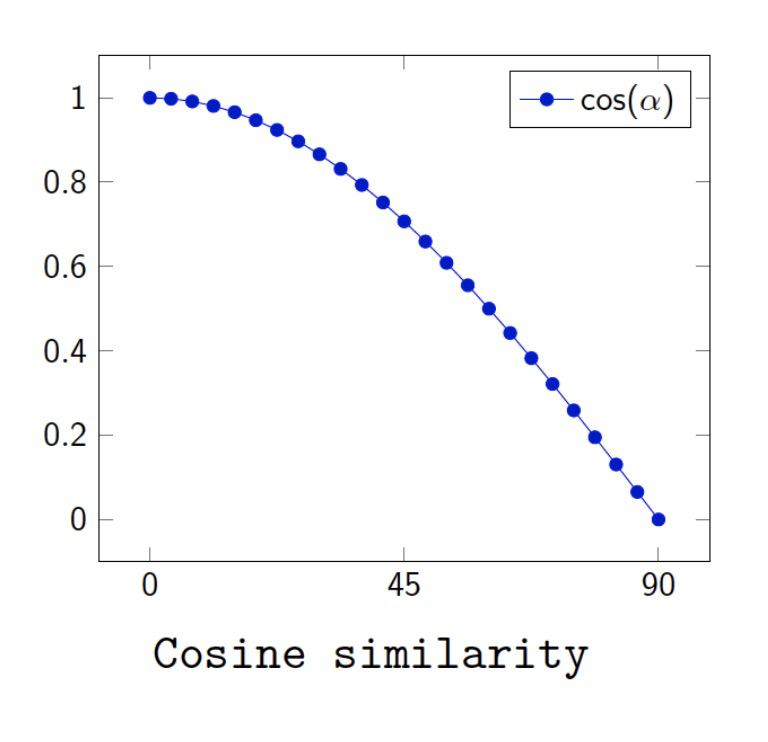
Why not euclidean distance? 为什么不用欧几里得距离
Euclidean distance is sensitive to the vector magnitude. 欧几里德距离对向量大小敏感,余弦相似度则不敏感。
(related to how many terms are in a document) Cosine similarity is not sensitive to vector magnitude.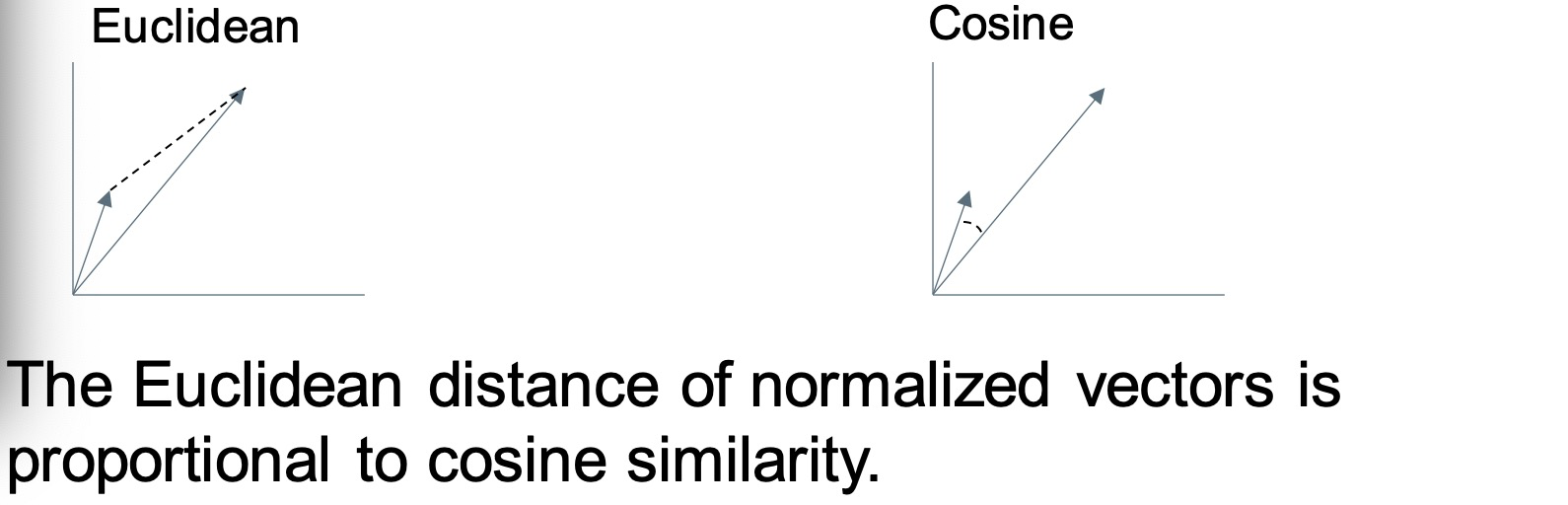
归一化向量的欧几里德距离与余弦相似度成正比
Example
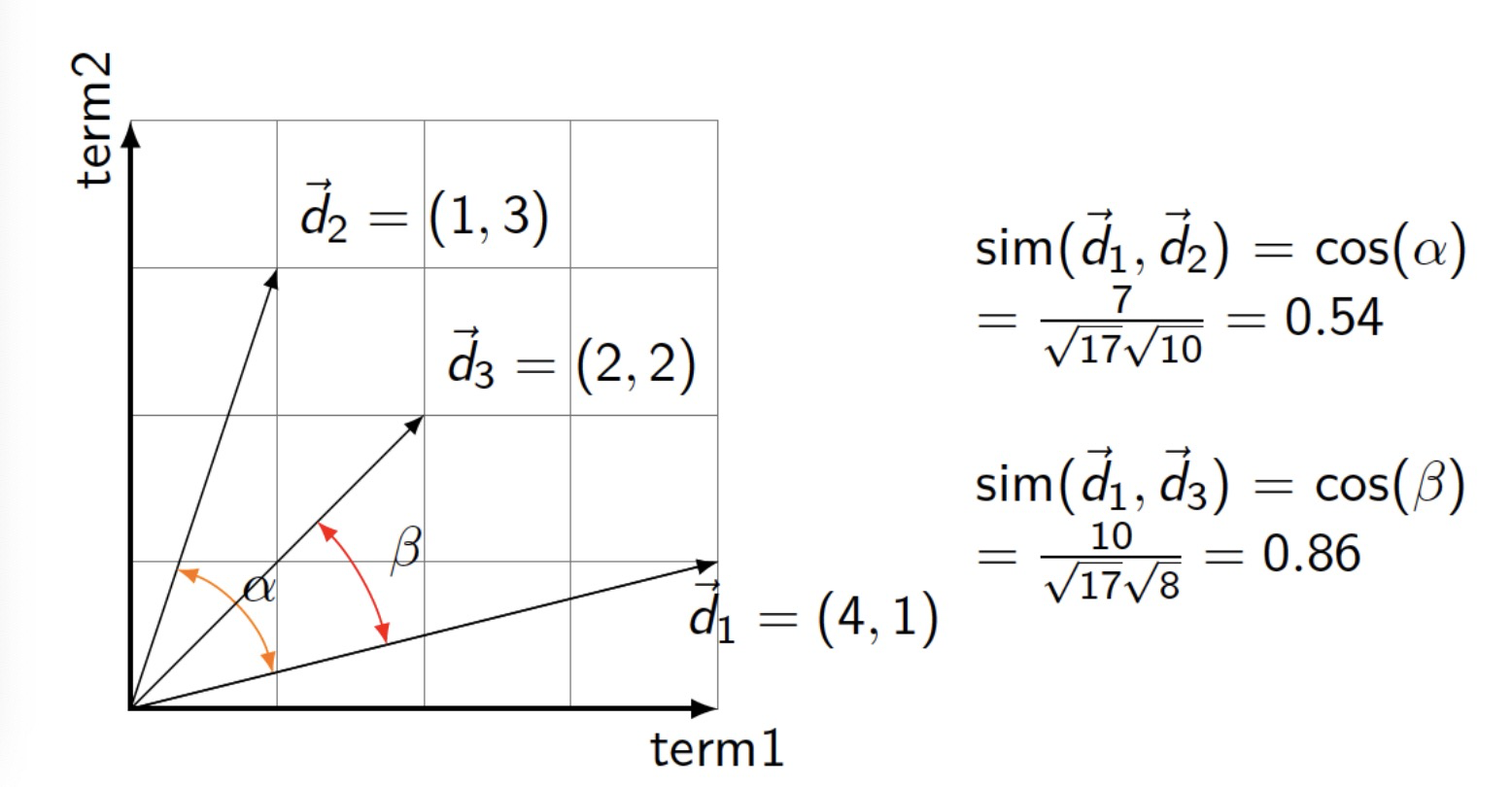
Cosine Similarity: Example with tf

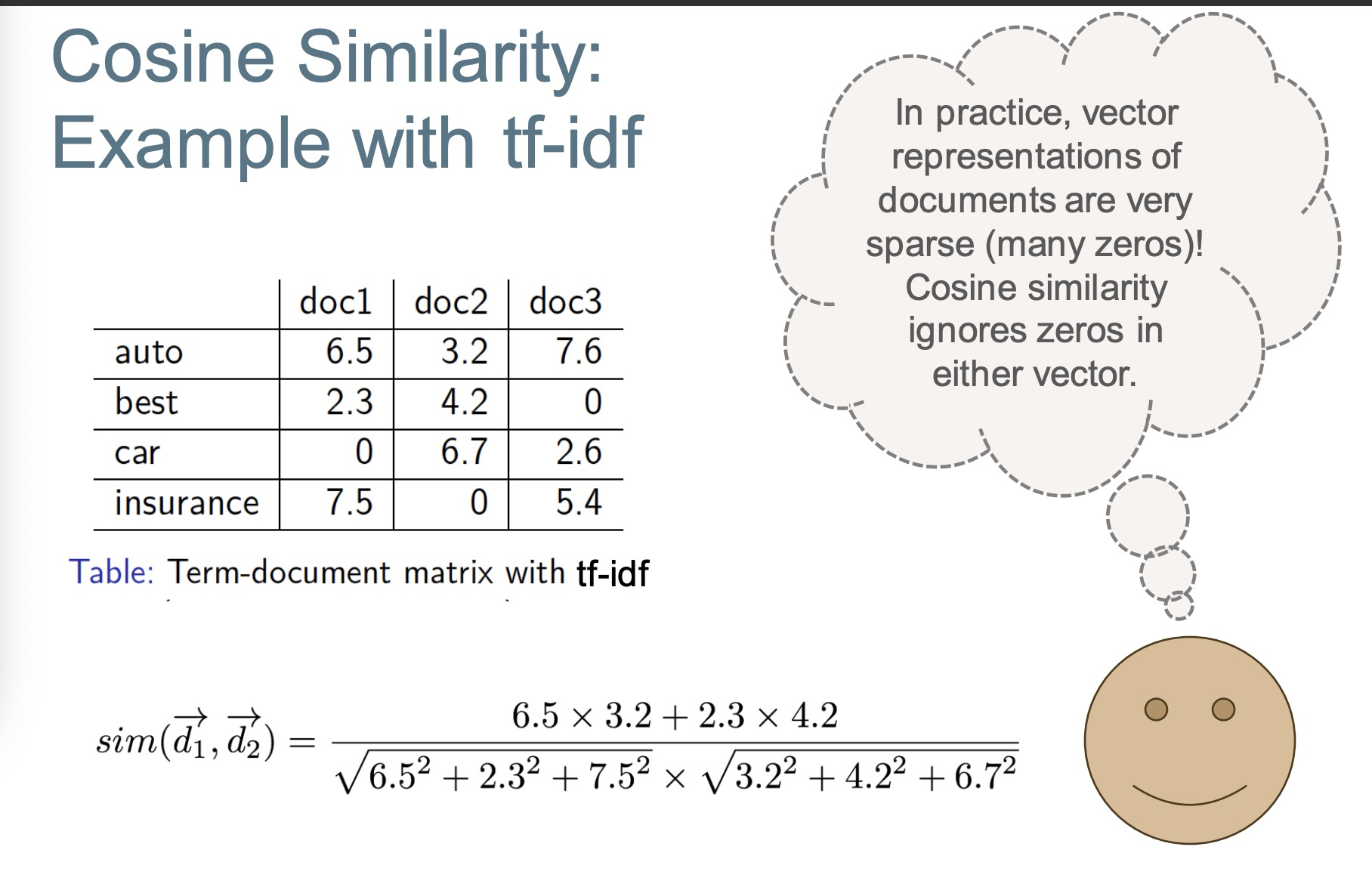
Query as a vector 查询语句变成向量
So far, we have represented documents as vectors 到目前为止, 我们把文档当作向量。
• The query can also be represented as a vector 查询语句也可以被当作向量
– Pretend it is a document (use query terms to construct vector)
– When using tf-idf the document frequency for the query vector comes from the document collection
• We can compute the similarity between the query vector and document vector using cosine similarity 我们可以计算查询语句向量和文档向量之间的余弦相似度
Score Function of Vector Space Model 向量空间模型的分数方程


