OWL Classes may be arranged into a taxonomic subclass hierarchy using the owl primitive rdfs:subClassOf
For example, for the problem of Michalski’s Trains we have 13 classes about trains. _Jagged _is a subclass of _Closed _which is a subclass of _Car _which is a subclass of the predefined owl:Thing.
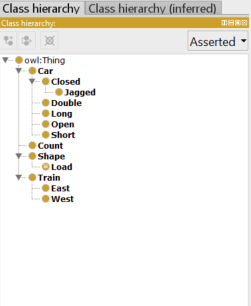
We can see the corresponding Turtle for the class relationship between Closed and Jagged, noting also the axioms stating that the classes Closed and Open are disjoint (i.e. no common individual members).
We can also describe Classes in more complex ways using object property relationships and class constructors such as owl:unionOf and owl:intersectionOf. We can also define a class to be exactly equal to another class using owl:equivalentClass. This can be used for a simple class name aliasing, but because it can equate complex class descriptions, it can also be a powerful axiom that needs to be interpreted by a formal logic _reasoner _in order to compute deductive inferences across the ontology.
我们可以看到封闭类和交错类之间的对应关系,也注意到了封闭类和开放类是不相交的公理(即没有共同的个体成员)。 我们还可以使用对象属性关系和类构造函数,比如owl:unionOf和owl:intersectionOf,以更复杂的方式描述类。我们还可以使用owl:equivalentClass将一个类定义为与另一个类完全相等。这可以用于简单的类名别名,但是因为它可以等同于复杂的类描述,所以它也可以是一个强大的公理,需要由形式逻辑推理机来解释,以便跨本体计算演绎推理。

