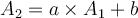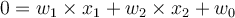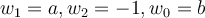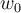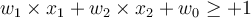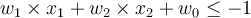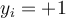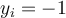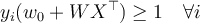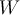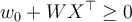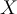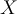Overview 概述
下图表示训练集tuple线性可分情况。
If the training tuples can be plotted as follows (x-axis and y-axis represent 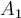 and
and 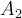 , respectively), then the dataset is linearly separable:
, respectively), then the dataset is linearly separable: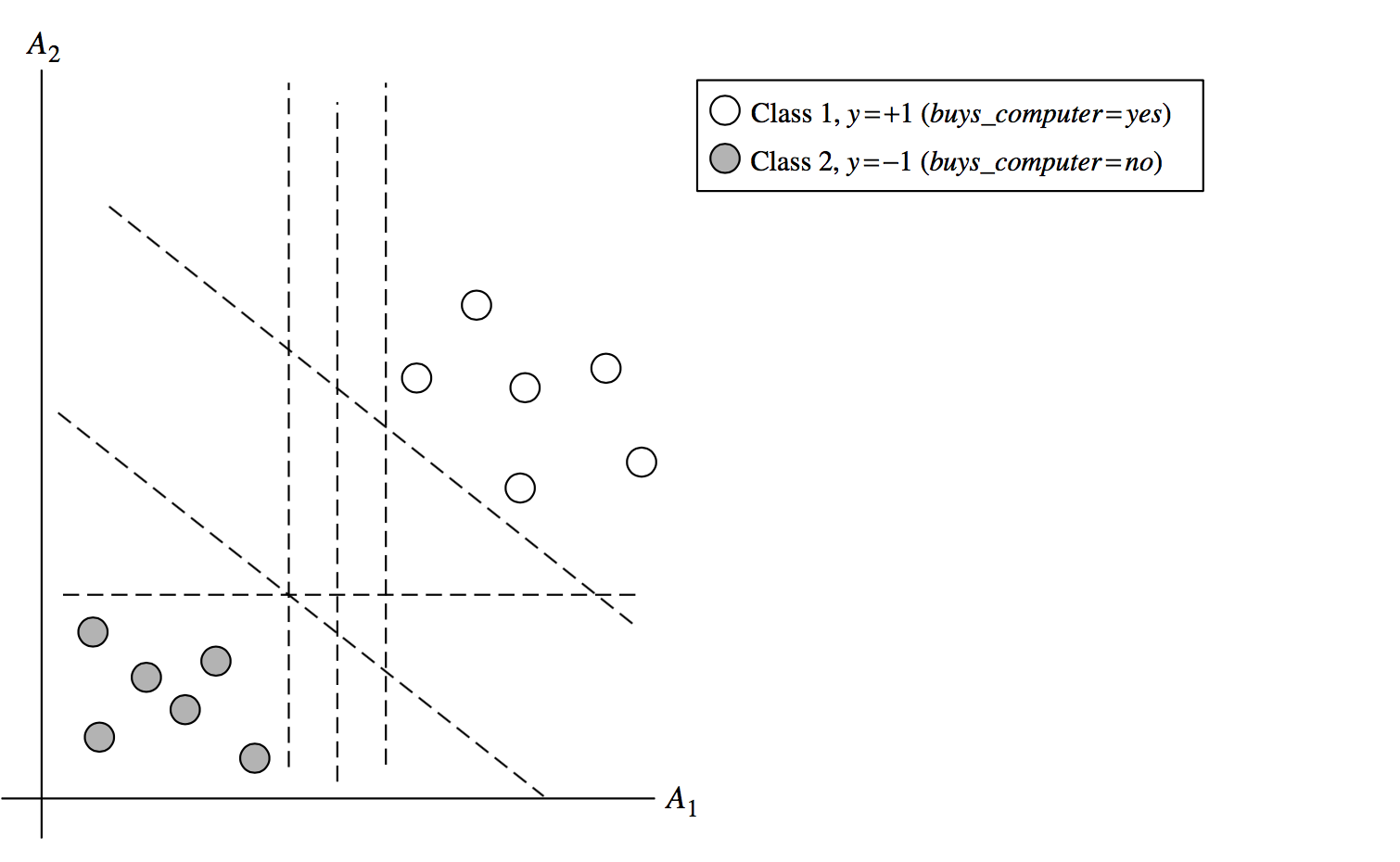
- Because a straight line (hyperplane) can be drawn to separate all the tuples of class +1 from all the tuples of class -1. 用一条直线可以分割开不同类别的训练集。
- There are infinite lines (hyperplanes) separating the two classes. 有无限种分割方法可以得到同样的分类结果。如上图
- e.g., all of the dotted lines separate the training tuples exactly the same in the above example.
- We want to find the best one (the one that minimises classification error on unseen data). 我们想要找到最好的分割方法。判别方法
Maximum marginal hyperplane 最大边界超平面
SVM searches for the hyperplane with the largest margin, i.e., maximum marginal hyperplane (MMH)
SVM搜索具有最大边际的超平面,即最大边际超平面(MMH)
- Margin: Draw a perpendicular line from the hyperplane to a tuple. The distance between the hyperplane and the tuple is the margin of that hyperplane.
边距:从超平面画一条垂线到元组。超平面和元组之间的距离就是超平面的边界。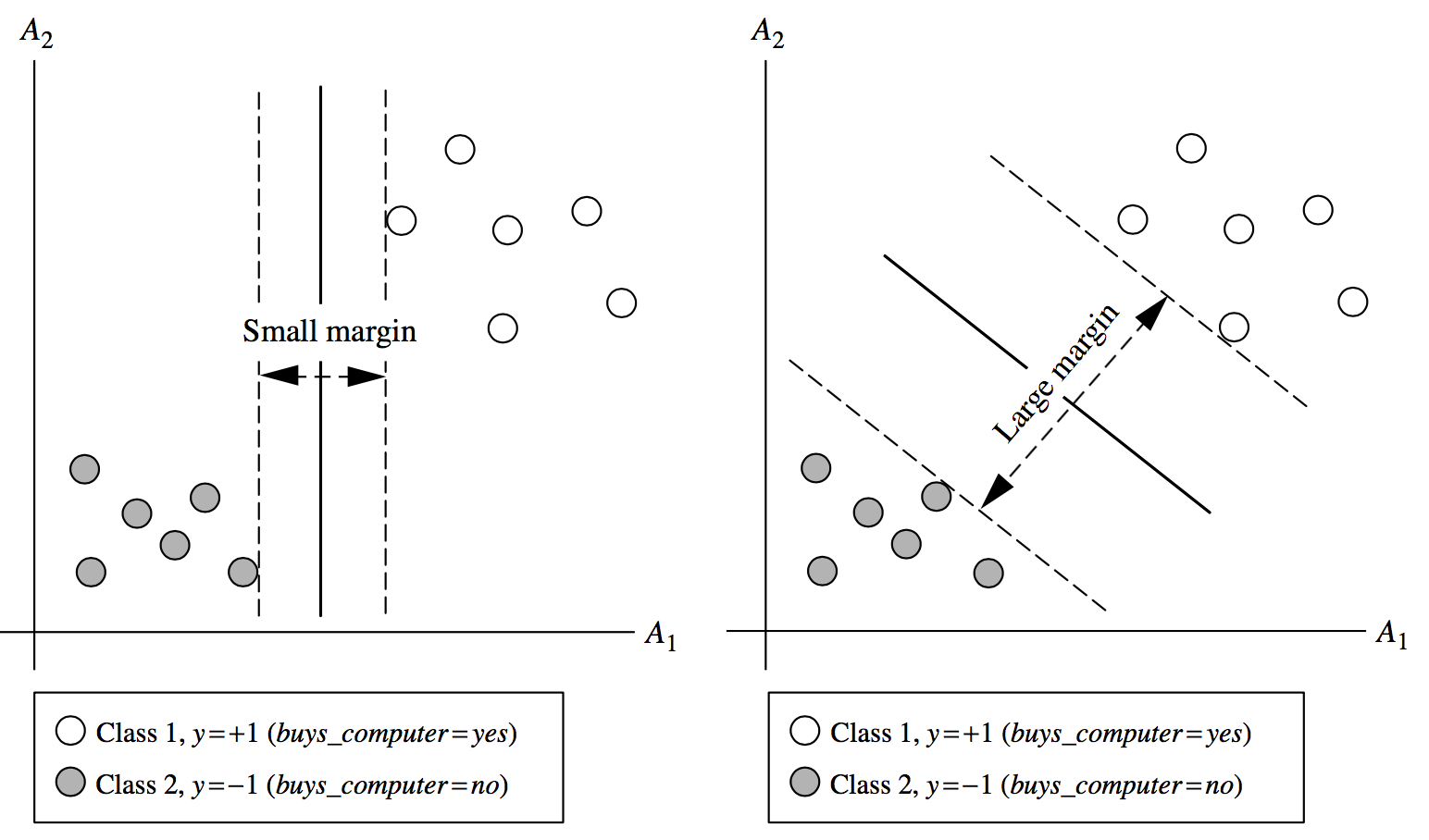
Support Vectors:
- Support vectors: the training tuples that determine the largest margin hyperplane. In the above example, red-circled tuples are the support vectors of the hyperplane.
支持向量:决定最大边界超平面的训练元组。在上面的例子中,红圈元组是超平面的支持向量。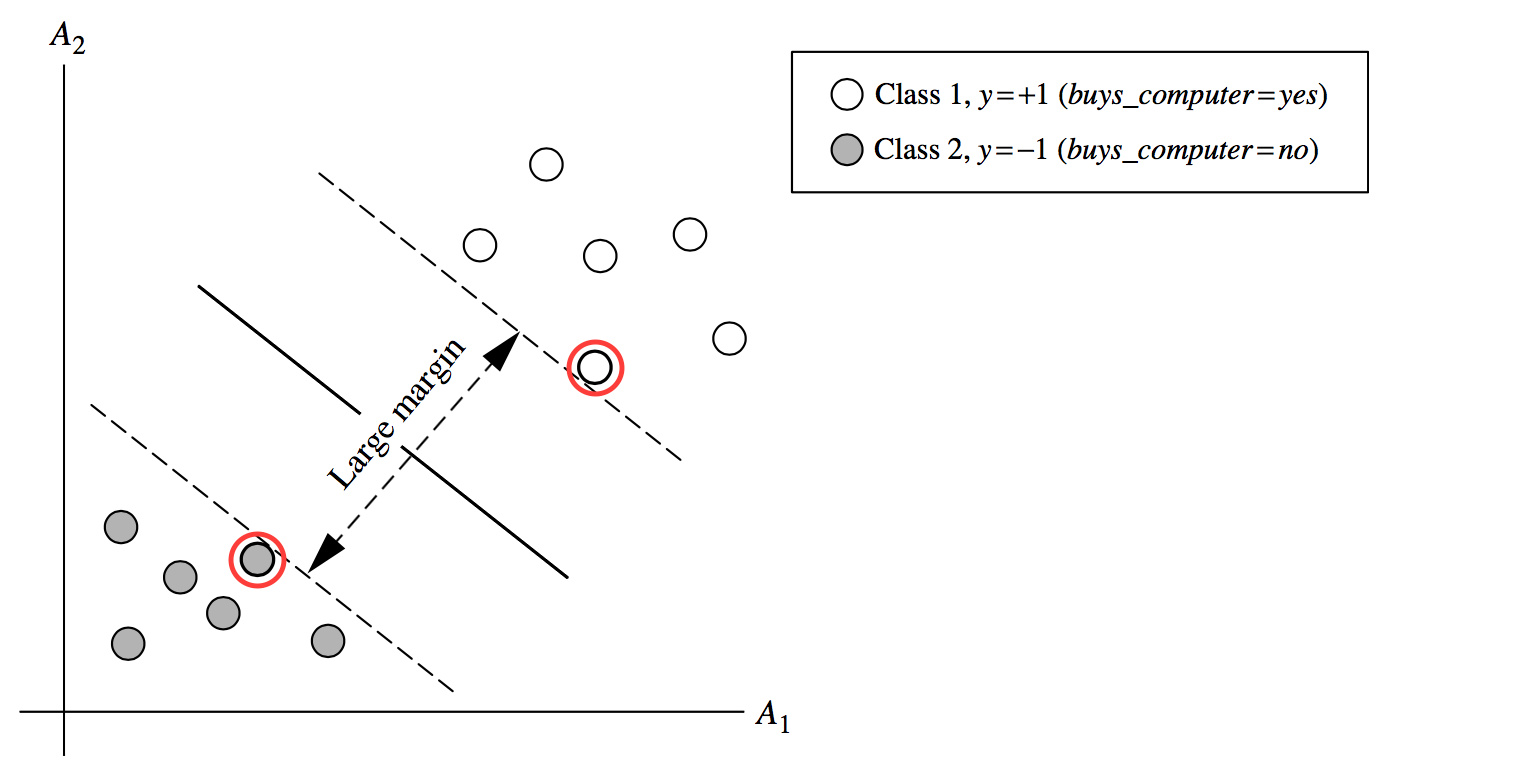
Formal definition of hyperplanes and support vectors:
Two dimensional training tuple case:
- In two dimensional space (
 plane), a hyperplane corresponds to a line, and every hyperplane can be written as:
plane), a hyperplane corresponds to a line, and every hyperplane can be written as:
- For a more general representation, if we replace
 and
and 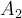 by
by 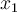 and
and 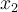 , then the above hyperplane can be rewritten as:
, then the above hyperplane can be rewritten as:
- In the linearly separable case, every training tuple satisfies the following condition:
- Support vector: Therefore, every training tuple that satisfies
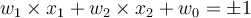 is a support vector.
is a support vector.
N-dimensional training tuple case:
- Let
 be a training tuple with class label
be a training tuple with class label 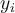 then a separating hyperplane can be written as
then a separating hyperplane can be written as 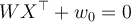
- where
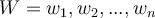 is a weight vector and
is a weight vector and  a scalar (bias)
a scalar (bias) The hyperplane defining the sides of the margin:
- These two equations can be combined into one equation:
Classify test tuple using trained model:
During the testing phase, the trained model classifies a new tuple 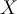 using the rules:
using the rules:
- Using hyperplane
- Alternatively, we can use the support vectors
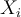 , each with class label
, each with class label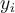 , to classify test tuples. For test tuple
, to classify test tuples. For test tuple 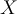 ,
, 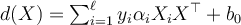
- where
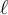 is the number of support vectors, and
is the number of support vectors, and  and
and 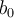 are automatically determined by the optimisation/training algorithm.
are automatically determined by the optimisation/training algorithm. - If the sign of
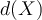 is positive then
is positive then 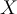 is classified as H1, otherwise H2.
is classified as H1, otherwise H2. - Note that we need to keep only the support vectors for testing
- This fact will be used in the non-linearly separable case
Why Is SVM effective on high-dimensional data?
- The complexity of a trained classifier is characterised by the number of support vectors rather than the dimensionality of the data
- The support vectors are the essential or critical training examples —they lie closest to the decision boundary (MMH)
- If all other training examples are removed and the training is repeated, the same separating hyperplane would be found from the support vectors alone
- The number of support vectors found can be used to compute an (upper) bound on the expected error rate of the SVM classifier, which is independent of the data dimensionality
- Thus, an SVM with a small number of support vectors can have good generalisation, even when the dimensionality of the data is high