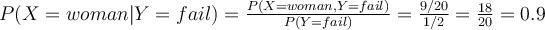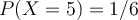Basic Probability Theory
    Before discussing probabilistic classifiers, we recap basic probability theory first.

    • EventBasic Probabilities - 图1: A subset of outcomes of an experiment (a subset of event space).
      • Let’s assume that we roll a dice with six faces. If we observe number 3 from a single roll, then 3 is the event, Basic Probabilities - 图2
      • A set of observations can also be an event, signifying any of the observations in the set. For example, an event from a dice roll Basic Probabilities - 图3 can signify the outcome that either 1, 3, or 5 is rolled.
    • Event space (sample space): the set of all possible outcomes
      • e.g. {1,2,3,4,5,6} with a six-faced dice
    • Probabilityof event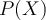Basic Probabilities - 图4: probability of observing an event
      • e.g. probability of observing 5 from a single dice roll, Basic Probabilities - 图5
    • Joint probability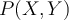Basic Probabilities - 图6: probability of observing multiple distinguishable events.
      • e.g. roll a dice and flip a coin, simultaneously. What would be the probability of observing 3 from the dice and HEAD from the coin Basic Probabilities - 图7?

    • Example
      For an experiment, we roll a dice and flip a coin simultaneously, and record the first six trials as follows: | Trial # | Dice | Coin | | —- | —- | —- | | 1 | 1 | H | | 2 | 2 | T | | 3 | 1 | T | | 4 | 3 | H | | 5 | 4 | H | | 6 | 1 | T |

    • Q: Given the above experiments, what is the probability of observing 3 from the dice?
      A: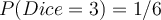 Basic Probabilities - 图8
      Q: Given above experiments, what is the probability of observing Dice={1,2} from the dice?
      A: Basic Probabilities - 图9
      Q: Given above experiments, what is the probability of observing 1 and TAIL from a single execution?
      A: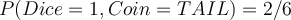 Basic Probabilities - 图10
      Conditional probability
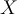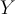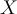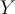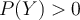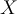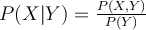      A conditional probability measures the probability of event Basic Probabilities - 图11 given that another event Basic Probabilities - 图12 has occurred. If Basic Probabilities - 图13 and Basic Probabilities - 图14 are events with Basic Probabilities - 图15, the conditional probability of Basic Probabilities - 图16 given Basic Probabilities - 图17 is Basic Probabilities - 图18.
      Example: Drug test
      Let’s assume that we have 4000 patients who have taken a drug test. The following table summarises the result of the drug test. We categorise the result based on gender and test result. | | Women | Men | | —- | —- | —- | | Success | 200 | 1800 | | Failure | 1800 | 200 |

    • Let
      Basic Probabilities - 图19 represent gender
      Basic Probabilities - 图20 represent a result of a drug test
      Then what is the probability of a patient being a woman when the patient fails on a drug test, i.e.,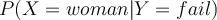 Basic Probabilities - 图21?
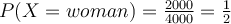
      Basic Probabilities - 图22
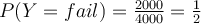
      Basic Probabilities - 图23
      Basic Probabilities - 图24
      From these probabilities, we can compute the conditional probability
      Basic Probabilities - 图25