Exercise: K-means clustering

Suppose that the data mining task is to cluster points (with (x,y) representing location) into three clusters, where the points are
.
The distance function is Euclidean distance. Suppose initially we assign 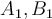, and 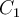as the center of each cluster, respectively. Use the k-means algorithm to show three clusters and their centres after the first round of execution.

Find the three cluster centres after the first round of execution.

Step 1: Centres are (1) A1 (2,10) , (2) B1(5,8), (3) C1(1,2) as given.
Step 2: Assign each object to nearest cluster by Euclidean distance from cluster centre
Object A2(2,5) is 5 from A1, sqrt(9+9) from B1, sqrt(1+9) from C1 so is assigned to cluster 3.
Object A3(8,4) is sqrt(36+36) from A1, sqrt(9+16) from B1, sqrt( 49+4) from C1 so is assigned to cluster 2.
Object B2(7,5) is sqrt(25+25) from A1, sqrt(4+9) from B1, sqrt(36+9) from C1 so is assigned to cluster 2.
Object B3(6,4) is sqrt(16+36) from A1, sqrt(1+16) from B1, sqrt(25+4) from C1 so is assigned to cluster 2.
Object C2(4,9) is sqrt(4+1) from A1, sqrt(2) from B1, sqrt(9+49) from C1 so is assigned to cluster 2.
Answer:
After the first round, the three new clusters are:
(1) {A1}, (2) {B1, A3, B2, B3, C2}, (3) {C1, A2},
and their new centres (step 3) are
(1) (2, 10)
(2) ((5+8+7+6+4)/5 = 6, ((8+4+5+4+9)/5 =6) = (6, 6)
(3) ((1+2) /2 = 1.5, (2+5) / 2=3.5) = (1.5, 3.5)

And something to ponder: When we have finished the k-means algorithm, what is cluster 1 going to look like? And what does this say for the effectiveness of k-means?