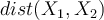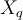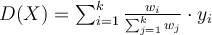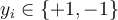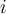• kNN classifiers are based on learning by analogy
  • A training tuple described by _n _attributes represents a point in the n-dimensional space
    • All training tuples are stored in an n-dimensional space
  • Given a tuple of unknown class or unknown target value, KNN classifier searches k nearest neighbours of the unknown tuple.
    • The nearest neighbours are defined in terms of Euclidean distance or other metrics, K-Nearest Neighbourhood (k-NN) - 图1

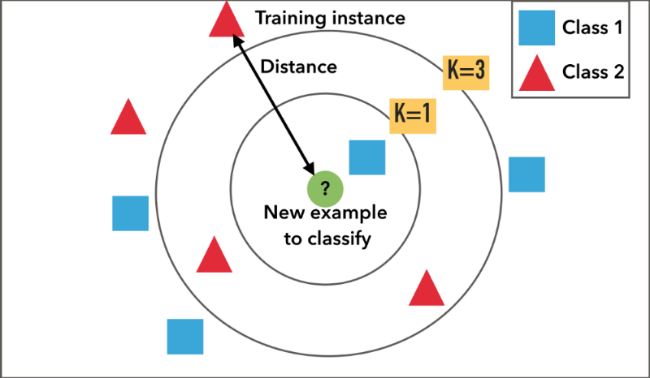
image.png

Two ways of classifying the unknown tuple in kNN

  • Discrete method (discrete-valued method)
    1. - k-NN returns the most common value among the k training examples nearest to [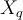![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425856202-fb275c26-a131-4ea2-81e6-074b5396f7b4.png#align=left&display=inline&height=20&margin=%5Bobject%20Object%5D&originHeight=20&originWidth=23&size=0&status=done&style=none&width=23)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=X_q) (test tuple)
    2. - Decision function: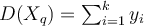
    3.    - [![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425858266-be25c9cc-ae43-47b1-9c17-9fe5671a1e4d.png#align=left&display=inline&height=26&margin=%5Bobject%20Object%5D&originHeight=26&originWidth=144&size=0&status=done&style=none&width=144)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=D%28X_q%29%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7Bk%7D%20y_i)
    4.    - wher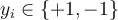e [![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425855895-d4211c4d-d2db-406e-bf2a-2f1b9b41ee7e.png#align=left&display=inline&height=20&margin=%5Bobject%20Object%5D&originHeight=20&originWidth=118&size=0&status=done&style=none&width=118)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=y_i%20%5Cin%20%5C%7B%2B1%2C%20-1%5C%7D) is the class of [![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425855620-5a45093c-807d-41f7-b793-ca0ab0312d10.png#align=left&display=inline&height=14&margin=%5Bobject%20Object%5D&originHeight=14&originWidth=6&size=0&status=done&style=none&width=6)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=i)th nearest neighbour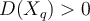
    5.    - If [![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425856142-ff99afd9-1db8-48a8-81cf-edc6fe918ff9.png#align=left&display=inline&height=21&margin=%5Bobject%20Object%5D&originHeight=21&originWidth=90&size=0&status=done&style=none&width=90)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=D%28X_q%29%20%3E%200) then [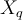![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623425855560-cbbb15f1-8716-494f-8078-390b2b349d03.png#align=left&display=inline&height=20&margin=%5Bobject%20Object%5D&originHeight=20&originWidth=23&size=0&status=done&style=none&width=23)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=X_q) is positive class otherwise negative class
    6. - Voronoi diagram: the decision surface induced by 1-NN for a typical set of training examples

image.png

  • Continuous method (real-valued prediction):
    • Returns the mean values of the k nearest neighbours
    • Distance-weighted nearest neighbour algorithm
      • Weight the contribution of each of the k neighbours according to their distance to the query K-Nearest Neighbourhood (k-NN) - 图4
      • Give greater weight to closer neighbours
        K-Nearest Neighbourhood (k-NN) - 图5
    • Decision function:
      • K-Nearest Neighbourhood (k-NN) - 图6
      • where K-Nearest Neighbourhood (k-NN) - 图7 is the target value of K-Nearest Neighbourhood (k-NN) - 图8th nearest neighbour

Characteristics of KNN

  • Robust to noisy data by averaging k-nearest neighbours
  • Extremely slow when classifying test tuples
    • With 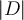K-Nearest Neighbourhood (k-NN) - 图9 training tuples, 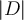K-Nearest Neighbourhood (k-NN) - 图10 comparisons are required to find k-nearest neighbourhood
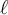    • For example, SVM only requires K-Nearest Neighbourhood (k-NN) - 图11 comparisons where K-Nearest Neighbourhood (k-NN) - 图12 is the number of support vectors
    • Partial distance method:
      • Compute a distance on a subset of n attributes.
        • If the distance exceeds a threshold, further distance computation will be halted
        • Otherwise keep computing the distance on the remaining attributes

部分距离方法:
计算n个属性子集上的距离。
如果距离超过一个阈值，进一步的距离计算将停止
否则，继续计算其余属性的距离