Boosting is when you generate different training sets by sampling with replacement. You are relying on the theory of bootstrapping improve the accuracy of a weak learner. Adaboost learns a sequence of classifiers, and weights both the vote for each classifier and the training set for the subsequent classifier based on accuracy. Let’s run through AdaBoost. 增强是指通过替换采样生成不同的训练集。你是靠自举理论提高一个弱学习者的准确率。Adaboost学习一系列分类器，并根据准确性对每个分类器的投票和后续分类器的训练集进行加权。让我们来看看AdaBoost。

    Assume a 1-dimensional training set of 2 classes of tuples (represented by their values here) D = + : {1, 2, 3} , - : { 4, 5}. 原始数据集
    Weight the training set uniformly, so assign weight 1/5 to each : WD1 = +: {1:1/5, 2:1/5, 3:1/5}, -: {4:1/5, 5:1/5}. 初始权重赋值。
    Now start the loop to learn a predetermined number of classifiers:
    Draw a weighted random sample with replacement from WD_1 to derive training set, say D_1 = +1,+1,+ 2, -4 -,4 (class label is shown together with the value here). 随机采样
    Using D_1 for training, learn a classifier, say M_1. Let’s say M_1 is the function _M_1(x) Ξ if x<=1 then “+” else “-“. _Note that this will classify the value 2 wrongly.
    Compute err(M1) _on its training set D_1 using the formula 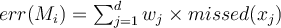Example: AdaBoost ensemble method - 图1 where missed(x) Ξ if x missclassified by M_1 then “1” else “0” 原权重 x 是否错误（错误为1）
    _ _so err(M_1) = 1/5 0 + 1/5 0 + 1/5 1 + 1/5 0 + 1/5 0 = 1/5
    Now update weights in WD_1 by multiplying correct tuples by by (err(M_1 ) / (1-err(M_1)) = (1/5) / (1- 1/5) = 1/4 and leaving the incorrect or unused tuples as they were. 更新正确类权重
    To get WD_1’ = +: {1:1/5     1/4 , 2:1/5 , 3:1/5}, -: {4:1/5 1/4, 5:1/5}. That is, WD_1’ = +: {1:1/20, 2:1/5 , 3:1/5}, -: {4:1/20, 5:1/5}.
    Now we need to normalise the weights in WD_1’ to add to 1. So compute the sum of the weights and divide all the weights by that sum. 将权重正则化 累加起来为1。
    Sum of weights in WD_1’ = 1/20+ 1/5 + 1/5 +1/20 +1/5 = 7/10
    New normalised WD_2 ready for next round, WD_2 = +: {1: (1/20)/(7/10), 2: (1/5)/(7/10) , 3: (1/5)/(7/10)}, -: {4: (1/20)/(7/10), 5: (1/5)/(7/10)}.
    That is, WD_2 = +: {1: 1/14), 2: 2/7) , 3: 2/7)}, -: {4: 1/14), 5: 2/7)}. Note how the weights for the correct answers of M_1, namely 1 and 4, are now very low.
    WD_2 is now our weighted training set ready for learning the next classifier M_2, and we go back to iterate the next round of the loop.
    Finally, we need to know how our classifiers will vote. Reusing err(M_1) =1/5 as calclulated above, we assign the weight of any vote by M_1 using the formula: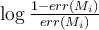
    Example: AdaBoost ensemble method - 图2 . For M_1 this is log((1-1/5)/(1/5)) = log(4) = 0.602. We use log to base 10 here, which is fine but convenient, although natural log is more common.
    Now, say we have learnt M_1, M_2 and M_3 with weights respectively of 0.6, 0.3, 0.4.
    What is the voted classification for unseen tuple 7?
    Say M_1 votes “-“ with weight 0.6. M_2 votes “+” with weight 0.3. M_3 votes “+” with weight 0.4.
    Compare the votes: 0.6 for “-“ and 0.7 for “+”. *Therefore the class “+” is assigned.