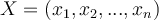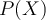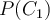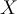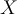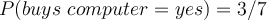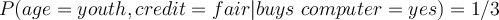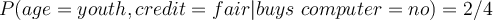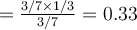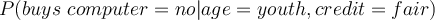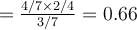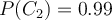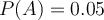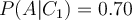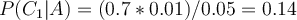Terminology
A running example**: Let’s assume that you are a owner of a computer shop. You may want to identify which customers buy a computer for targeting your advertising. So you decide to record a customer’s age and credit rating whether the customer buys a computer or not for future predictions.
- Evidence
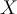 : A Bayesian term for observed data tuple, described by measurements made on a set of
: A Bayesian term for observed data tuple, described by measurements made on a set of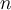 attributes.
attributes.
- Hypothesis
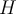 : A target of the classification. Hypothesis such that
: A target of the classification. Hypothesis such that belongs to a specified class
belongs to a specified class .
.
- Priorprobability,
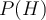 : the_a prioriprobability _of
: the_a prioriprobability _of 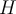
- Likelihood,
 : the probability of observing the sample
: the probability of observing the sample 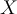 given that the hypothesis holds.
given that the hypothesis holds.
- Posteriorprobability,
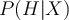 : the_a posteriori probability, _that is the probability that the hypothesis holds given the observed data
: the_a posteriori probability, _that is the probability that the hypothesis holds given the observed data . 后验概率:后验概率,即假设在给定观测数据的情况下成立的概率。
. 后验概率:后验概率,即假设在给定观测数据的情况下成立的概率。
The prediction of a class for some new tuple 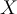 for which the class is unknown, is determined by the class which has the highest posterior probability. 类别的预测由具有最高后验概率的类别确定。
for which the class is unknown, is determined by the class which has the highest posterior probability. 类别的预测由具有最高后验概率的类别确定。
Bayes’ Theorem
In many cases, it is easy to estimate the posterior probabilty through estimating the prior and likelihood of given problem from historical data (i.e a training set).
- E.g., to estimate the prior
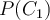 , we can count the number of customers who bought a computer and divide it by the total number of customers.
, we can count the number of customers who bought a computer and divide it by the total number of customers. - E.g., to estimate the likelihood
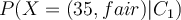 , we can measure the proportion of customers whose age is 35 and have _fair _credit rating among the customers who bought a computer.
, we can measure the proportion of customers whose age is 35 and have _fair _credit rating among the customers who bought a computer. - E.g., to estimate the evidence
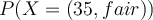 we can measure the proportion of customers whose age is 35 and have fair _credit rating amongst _all the customers, irrespective of computer-buying.
we can measure the proportion of customers whose age is 35 and have fair _credit rating amongst _all the customers, irrespective of computer-buying. - The posterior probability can then be computed from the prior and likelihood through Bayes’ theorem.
Bayes’ theorem provides a way to relate likelihood, prior, and posterior probabilities in the following way, when 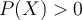

Informally, this equation can be interpreted as
Posterior = likelihood x prior / evidence
Bayes’ theorem is used to predict
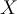 belongs to
belongs to  iff the posterior
iff the posterior  is the highest among all other
is the highest among all other 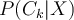 for all the k classes. We can also state the probability that
for all the k classes. We can also state the probability that 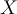 belongs to
belongs to 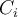 is
is 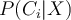 . Because we can give this probability, we call Bayes classification a probablistic classifier.
. Because we can give this probability, we call Bayes classification a probablistic classifier. - For determining the classification of some
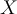 , we are looking to find the
, we are looking to find the 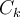 that maximises
that maximises  yet
yet  is the same for every
is the same for every 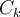 , so
, so  can be ignored in all the calculations as long as we don’t need to know the probability.
can be ignored in all the calculations as long as we don’t need to know the probability.
Example: with training data
Let’s assume that you are a owner of a computer shop. You may want to identify which customers buy a computer for a targeted advertisement. So the owner decided to record a customers’s age and credit rating no matter the customer buys a computer or not. The following table shows a set of customer records in the computer shop. What is the probability of a customer who is youth and has fair credit rating buying a computer?
| age | credit | buys_computer |
|---|---|---|
| youth | fair | no |
| youth | fair | yes |
| middle_aged | excellent | yes |
| middle_aged | fair | no |
| youth | fair | no |
| middle_aged | excellent | no |
| middle_aged | fair | yes |
- Prior: probability of a customer buying a computer regardless of their information.
- Likelihood
- Evidence
- Posterior
- Therefore, the customer would not buy a computer
- When computing a posterior, the evidence term is the same for all hypothesis classes. Since our goal is to find the highest class, the evidence term is often ignored in practice.
Example: with estimated probabilities
You might be interested in finding out a probability of patients having liver cancer if they are an alcoholic. In this scenario, we discover by using Bayes’ Theorem that “being an alcoholic” is a useful diagnostic examination for liver cancer.
- Prior:
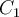 means the event “Patient has liver cancer.” Past data tells you that 1% of patients entering your clinic have liver disease.
means the event “Patient has liver cancer.” Past data tells you that 1% of patients entering your clinic have liver disease.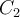 means the event “Patient does not have liver disease”.
means the event “Patient does not have liver disease”.
- Evidence:
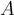 could mean the examination that “Patient is an alcoholic.” Five percent of the clinic’s patients are alcoholics.
could mean the examination that “Patient is an alcoholic.” Five percent of the clinic’s patients are alcoholics.
- Likelihood: You may also know from the medical literature that among those patients diagnosed with liver cancer, 70% are alcoholics.
- Bayes’ theorem tells you: If the patient is an alcoholic, their chances of having liver cancer is 0.14 (14%). This is much more than the 1% prior probability suggested by past data.