Multiple Linear Regression

Multiple Linear Regression 多元线性回归

In many applications, it is more general to have more than one predictor variable.
Multiple linear regression is a direct extension of the linear regression model.
Let’s assume that we have 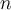predictor variables for each response variable, i.e., .
In the multiple linear regression model, the relation between a response variable and predictor variables are modelled as: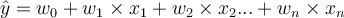

Again, parameters 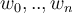can be estimated in least square fashion:

A least square method will find optimal parameters to minimise the squared error .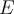
Significance of the weight
Most regression libraries or programs support significance testing for each weight. Usually, significant weights are denoted by * (or or depending on the significance level).
The significant attributes indicate that the effect (or influence) of the attribute is not just random! In other words, those significant attributes have high influence on predicting your response variable. This alone may be valuable information, even if you discard the linear model itself. 这些重要属性对预测你的反应变量有很大的影响。即使您抛弃线性模型本身，这一项本身也可能是有价值的信息
*Performance evaluation 与普通线性回归相同
The methods for evaluation of simple linear regression apply straightforwardly to the multiple variable case.