Contents
• Clustering overview
• K-Means
• Evaluating clustering
Unsupervised Learning 非监督学习
What if we don’t have labeled data? 如果我们没有带标签的数据怎么办
Then we are doing unsupervised learning 使用非监督学习
Can we still assign reasonable labels?
– We could try to cluster documents (cluster = class) 我们可以尝试聚类分析文档
– Clustering is a type of unsupervised learning 聚类分析是一种非监督学习
Other types of unsupervised learning (not covered in this course): 其它类型的非监督学习
- Autoencoders, Rule Mining, PCA 自动编码器,规则挖掘,主成分分析
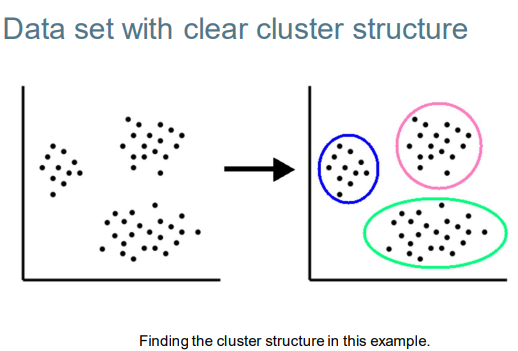
Clustering: Definition 聚类分析:定义
(Document) clustering is the process of grouping a set of documents into clusters of similar documents. (文档)聚类是将一组文档分组为相似文档簇的过程。 集群内的文档应该相似。
• Documents within a cluster should be similar. 集群内的文档应该相似。
• Documents from different clusters should be dissimilar. 来自不同集群的文档应该不同。
• Clustering is a very common form of unsupervised learning.聚类是一种非常常见的无监督学习形式。
Classification vs. Clustering 分类 vs 聚类
• Classification: supervised learning 分类:监督学习
• Clustering: unsupervised learning 聚类:非监督学习
• Classification: Classes are human-defined and part of the input to the learning algorithm. 分类:类别是认为定义的,是学习算法的一部分
• Clustering: Clusters are inferred from the data without human input. 聚类:聚类是由数据推导的,没有人为的输入。
– There are many ways of influencing the outcome of clustering: number of clusters, similarity measure, representation of documents, algorithm hyperparameters 影响聚类结果的方式有很多:聚类数量、相似性度量、文档表示、算法超参数
Desiderata for clustering 聚类的需要
• General goal: put related docs in the same cluster, put unrelated docs in different clusters. 将相关的文档放在同一个聚类下,不同的放在不同的聚类下
– How do we formalize this?
• The number of clusters should be appropriate for the data set we are clustering. 聚类的数量应该适合于我们正在聚类分析的数据集
– Initially, we will assume the number of clusters K is given. 初始化,假设聚类的数量K已经给定
– Ther are (semi)automatic methods for determining K 也有自动设定聚类数量k的方法
• Secondary goals in clustering (not always necessary) 聚类中的次级目标(非必要)
– Avoid very small and very large clusters 避免非常小或者非常大的聚类
– Defined clusters that are easy to explain to the user 定义容易向用户解释的聚类
Flat vs. Hierarchical clustering 平面集群与分层集群
• Flat algorithms 平面算法
– Usually start with a random (partial) partitioning of docs into groups 通常从随机部分将文档分组开始
– Refine iteratively 迭代优化
– Common algorithm: K-means 通常算法:k均值
• Hierarchical algorithms 分层级算法
– Create a hierarchy 创建层次结构
• Cluster the clusters 聚类分析
– Bottom-up, agglomerative 自下而上,聚集
– Top-down, divisive 自上向下,分裂
Hard vs. Soft clustering
• Hard clustering: Each document in exactly one cluster. 每个文档应该在一个确定的聚类中
– More common and generally easier to do 更通用和简单的做法
– Example algorithm: K-means 通常算法:k均值
• Soft clustering: A document is assigned a membership probability for each cluster. 为文档分配每个集群的成员概率
– A higher score means the document is: more likely to belong to that cluster or exhibit characteristics of that cluster 更高分分数意味着该文档可能属于这个聚类,或者表现出该聚类的特征
– Documents belong to multiple clusters 文档属于多个聚类
– Example algorithm: Gaussian Mixture Models (via EM) 算法:Gaussian Mixture Models (via EM)
We will only consider flat, hard clustering in this course 只学习hard clustering
Flat clustering algorithms 平面聚类算法
Flat algorithms compute a partition of N documents into a set of K clusters. 平面算法将N个文档划分成一组K个簇。
• Given: a set of documents and the number K 给定:文档库+聚类数量K
• Find: a partition into K clusters that optimizes the chosen partitioning criterion 将分区划分为K个集群,优化所选的分区标准
• Global optimization: exhaustively enumerate partitions, pick optimal one 全局优化:详尽列举分区,选择最佳分区
• Effective heuristic method: K-means algorithm 有效的启发式方法:K-均值算法
Document representation for clustering 聚类的文档表示
• Represent documents as vectors 将文档用向量表示
– Sparse count vectors, LSA, aggregated word2vec, Pre-trained language model (e.g. BERT) 稀疏计数向量、LSA、聚合单词2、预先训练的语言模型(例如BERT)
• We can measure similarity between vectors by Euclidean distance which is almost equivalent to cosine distance. 我们可以通过欧几里得距离来衡量向量之间的相似性,欧几里得距离几乎等同于余弦距离。
– Except: cosine distance is length-normalized
• Some clustering algorithms (e.g. Affinity propagation) only require similarities between documents (e.g. edit distance) 一些聚类算法(例如相似性传播)只要求文档之间的相似性(例如编辑距离)
Centroids in K-means k均值算法的质心
• Each cluster in K-means is defined by a centroid. k均值法中的每个聚类都有质心定义
• Definition of centroid: 
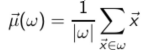
where we use ω to denote a cluster. 这里我们用ω来表示一个簇。
• Centroids act as centers of gravity, abstractions of the class质心作为重心,是类的抽象
K-means
• Objective/partitioning criterion: minimize the average squared difference from the centroid 目标/划分标准:最小化与质心的平均平方差
• We try to find the minimum average squared difference by iterating two steps: 我们尝试通过迭代两个步骤来找到最小平均平方差:
–Reassignment: assign each vector to its closest centroid 重新分配:将每个向量分配到其最近的质心
– Re-computation: recompute each centroid as the average of the vectors that were assigned to it 重新计算:将每个质心重新计算为分配给它的向量的平均值


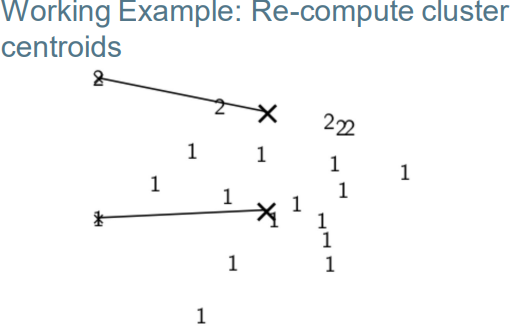
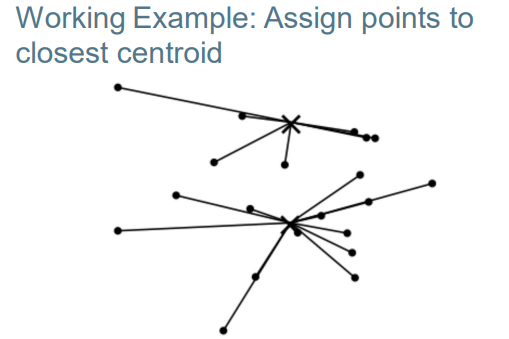

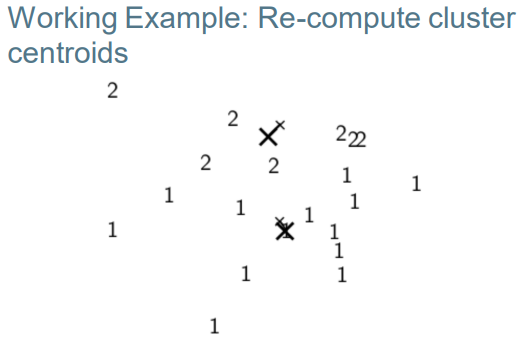
K-means algorithm k均值算法

K-means is guaranteed to converge k均值方法可以保证收敛
• RSS(residual sum of squares) = sum of all squared distances between document vector and closest centroid 文档向量和最近质心之间所有平方距离的总和
• RSS decreases during each reassignment step. – because each point is assigned to a closer centroid 在每个重新分配步骤中,RSS会降低。–因为每个点都被分配给一个更接近的质心
• RSS decreases during each re-computation step. – see next slide
• There are only a finite number of clusterings 集群数量有限
• Thus: We must reach a fixed point.因此:我们必须达到一个固定点。
Re-computaton decreases average distance
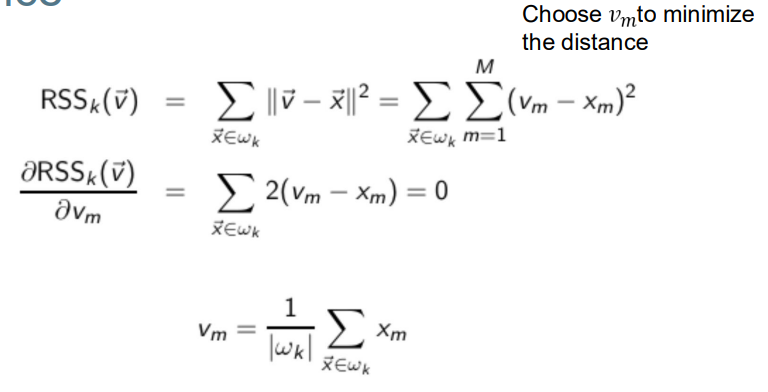
Re-computaton decreases average distance
K-means is guaranteed to converge k均值保证收敛
• But we don’t know how long convergence will take! 但是我们不知道需要多长时间才可以收敛
• If we don’t care about a few docs switching back and forth, then convergence is usually fast (< 10- 20 iterations). 如果我们不在乎一些文档的来回切换,那么收敛通常会很快(< 10- 20次迭代)。
• However, complete convergence can take many more iterations. 但是如果是完全收敛则会需要更多的迭代
Optimality of K-means k均值的最优性
• Convergence does not mean that we converge to the optimal clustering! 收敛并不意味着我们收敛到了最优聚类
• This is the great weakness of K-means. 这是k均值方法最大的劣势
• If we start with a bad set of seeds, the resulting clustering can be terrible. 如果我们以一个坏的初始开始,那聚类可能效果很差
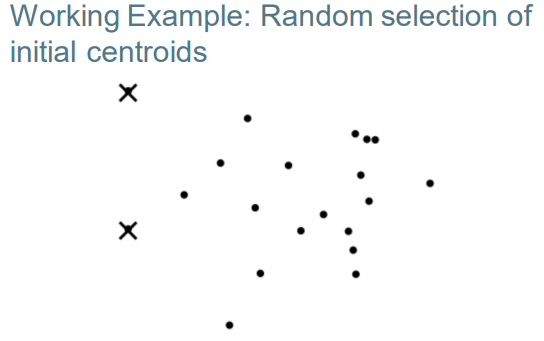
Initialization of K-means k均值方法的初始化方法
• Random seed selection is just one of many ways K-means can be initialized. 随机选择只是众多k均值初始化的方法之一
• Random seed selection is not very robust: It’s easy to get a suboptimal clustering. 随机选择法的鲁棒性不好,很容易得到次优聚类。
• Better ways of computing initial centroids: 更好的初始化质心点的方法
– Select seeds using a heuristic (e.g., ignore outliers or find a set of seeds that has “good coverage” of the document space) 使用启发式方法选择种子(例如,忽略异常值或找到一组对文档空间具有“良好覆盖”的种子)
– Use hierarchical clustering to find good seeds 使用层次聚类来寻找好种子
– Select i (e.g., i = 10) different random sets of seeds, do a K-means clustering for each, select the clustering with lowest RSS 选择I(例如,i = 10)个不同的随机种子集,对每个种子集进行K均值聚类,选择RSS最低的聚类
Evaluation 评估
• Internal criteria 内部标准
– Example of an internal criterion: RSS in K-means 内部标准示例:千位平均值中的RSS
• But an internal criterion often does not evaluate the actual utility of a clustering to an application. 但是内部标准通常不会评估集群对应用程序的实际效用。
• Alternative: External criteria 备选方案:外部标准
– Evaluate with respect to a human-defined classification根据人类定义的分类进行评估
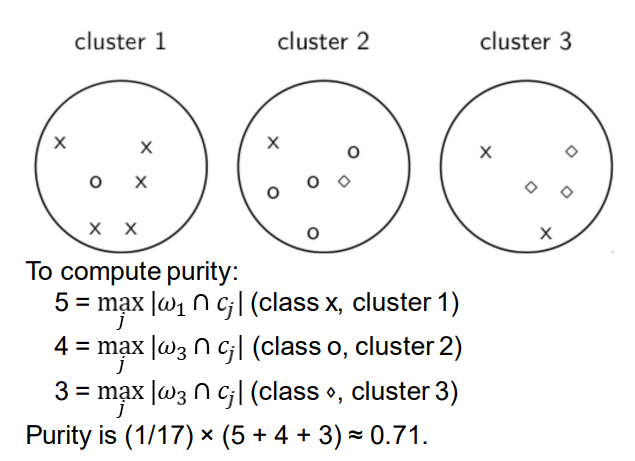
External criterion: Purity 外部标准:纯净度
如果我们有真实值,我们可以用纯净度来衡量

正确分类的点除以总点数
Example for computing purity
How many clusters?
• Number of clusters K is given in many applications. 在许多应用中给出了簇数K。
– E.g., there may be an external constraint on K. Example: In the case of web search results, it might be optimal for the users to present more than 10 -15 topics. 例如,k可能有外部限制。示例:在网络搜索结果的情况下,用户最好呈现10 -15个以上的主题。
• What if there is no external constraint? Is there a “right” number of clusters?
• One way: define an optimization criterion that penalizes a larger number of clusters 一种方法:定义一个对大量集群不利的优化标准
– Given docs, find K for which the optimum is reached. 给定文档,找到达到最佳的K。
– We can’t use RSS or average squared distance from centroid as the criterion because it would always choose K = N clusters 我们不能使用RSS或距质心的平均平方距离作为标准,因为它总是选择K = N个聚类

