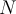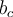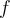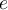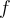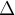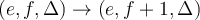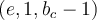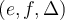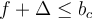Motivating Example

Say you’re looking at the traffic for Facebook profiles. You have billions of hits. You want to find which profiles are accessed the most often. You could keep a count for each profile, but then you’d have a very large number of counts to keep track of, the vast majority of which would be meaningless.
From https://stackoverflow.com/questions/8033012/what-is-lossy-counting
Frequent-pattern mining finds a set of patterns that occur frequently in a data set, where a pattern can be a set of items (called an itemset). A pattern is considered frequent if its count satisfies a minimum support.
Many frequent-pattern mining algorithms require the system to scan the whole data set more than once, but this is unrealistic for data streams.
We introduce one algorithm: the Lossy Counting algorithm有损技术算法. It approximates the frequency of items or itemsets within a user-specified error bound, 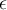Frequent Pattern Mining - 图1. 它近似于用户指定的错误界限内的项目或项目集的频率。
We illustrate the concept of lossy counting as follows:
Approximate frequent items 近似频繁项. You are interested in all profiles whose frequency is at least 1% (min support) of the entire Facebook traffic seen so far. It is felt that 1/10 of min support (i.e., 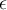Frequent Pattern Mining - 图2 = 0.1%) is an acceptable margin of error. This means that all frequent items with a support of at least 1% (min support) will be found, but that some items with a support of only at least (min support − 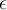Frequent Pattern Mining - 图3 ) = 0.9% will also be output.

Lossy Counting Algorithm

Definitions

  • We first need to set our margin of error 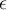Frequent Pattern Mining - 图4 between 0 and 1. 讲误差幅度设置在0到1之间。
  • The incoming stream is conceptually divided into buckets of width 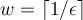Frequent Pattern Mining - 图5 transactions each. 宽度为 w=1/e 的桶
    • This is a conceptual bucket! We will not store all items from the incoming stream. 这是概念桶，我们不会在其中储存任何数据流。
  • Buckets are labeled with bucket ids, starting from 1. 桶会被标记上id，从1开始
  • Let 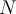Frequent Pattern Mining - 图6 be the current stream length (the index of last item in the stream). N为当前流的长度
  • The current bucket id of 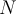Frequent Pattern Mining - 图7th item is 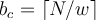Frequent Pattern Mining - 图8. 当前流的桶id为 【N/w】
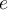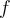  • For an element Frequent Pattern Mining - 图9, we denote its frequency in the stream by Frequent Pattern Mining - 图10.
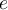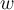  • Note that Frequent Pattern Mining - 图11 and Frequent Pattern Mining - 图12 are fixed e 和 w 是固定的
    • while Frequent Pattern Mining - 图13, Frequent Pattern Mining - 图14 and Frequent Pattern Mining - 图15 are running variables whose values change as the stream progresses.
  • Our data structure 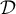Frequent Pattern Mining - 图16, is a set of triples of the form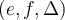 Frequent Pattern Mining - 图17
    • Frequent Pattern Mining - 图18 is an element in the stream e是流中的元素
    • Frequent Pattern Mining - 图19 is an integer representing its estimated frequency f是其估计频率的整数
    • Frequent Pattern Mining - 图20 is the maximum possible error in Frequent Pattern Mining - 图21. 最大错误概率

Algorithm:

  1. Initially, 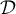Frequent Pattern Mining - 图22 is empty. 初始化，数据集D是空
  2. Whenever a new element 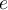Frequent Pattern Mining - 图23 arrives, we first lookup 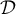Frequent Pattern Mining - 图24 to see whether an entry for 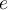Frequent Pattern Mining - 图25 already exists or not.每次拿到一个新元素e，我们去数据集D中查看是否有元素e已经存在。
    1. If lookup succeeds, we update the entry by incrementing its frequency Frequent Pattern Mining - 图26 by one. 如果查找成功， 则把其频率f+1 Frequent Pattern Mining - 图27
    2. Otherwise, we create a new entry of the form Frequent Pattern Mining - 图28. 否则我们创建一个新的 entry， 频率为1.
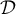  3. We prune Frequent Pattern Mining - 图29 by deleting some of its entries whenever 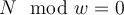Frequent Pattern Mining - 图30. 我们可以给数据集D剪枝，去除N除以w 余数为0 的桶
    • Deletion rule: an entry Frequent Pattern Mining - 图31 is deleted if Frequent Pattern Mining - 图32. 如果频率+最大容错率小于桶id 则删去。
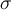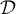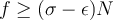  4. When a user request a list of item with min support Frequent Pattern Mining - 图33, we output those entries in Frequent Pattern Mining - 图34 where Frequent Pattern Mining - 图35.

Note that we delete item 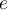Frequent Pattern Mining - 图36 based on the deletion rule in step 3. If the deleted item 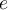Frequent Pattern Mining - 图37 appears again in the stream later on, the frequency 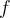Frequent Pattern Mining - 图38 of the item will re-start from 1. (step 2-2) 步骤3中删除的项目若再次出现在流中，则重新从1开始计算频率。
Example:
Let 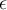Frequent Pattern Mining - 图39 be 0.1. Then the size of each bucket is 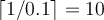Frequent Pattern Mining - 图40. 最小支持 为0.1
From a data stream, we first observed following 10 elements: 从一个数据流中我们观测到了如下十个元素。
(e1, e2, e1, e3, e4, e5, e1, e2, e6, e1)
Then the lossy counting data structure 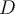Frequent Pattern Mining - 图41 should keep following triples: 有损计数算法数据结构D应该有一下元组
(e1, 4, 0)
(e2, 2, 0)
(e3, 1, 0)
(e4, 1, 0)
(e5, 1, 0)
(e6, 1, 0)
Given these triples, the algorithm starts pruning(step3) because 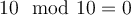Frequent Pattern Mining - 图42.
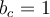By the deletion rule, we only keep the following triples in Frequent Pattern Mining - 图43 (note that Frequent Pattern Mining - 图44):
(e1, 4, 0)
(e2, 2, 0)
If the 11th element will be e3, then the updated 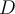Frequent Pattern Mining - 图45 will contain:
(e1, 4, 0)
(e2, 2, 0)
(e3, 1, 1)
because 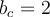Frequent Pattern Mining - 图46 for the 11th element.

Error Analysis

How much can a frequency count be underestimated?
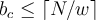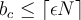An item is deleted when Frequent Pattern Mining - 图47 for an item. We know Frequent Pattern Mining - 图48 that is Frequent Pattern Mining - 图49.
The actual frequency of an item is at most 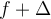Frequent Pattern Mining - 图50.
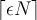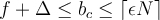Therefore the most that an item can be underestimated is Frequent Pattern Mining - 图51 (because Frequent Pattern Mining - 图52).
If the actual support of a removed item is 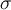Frequent Pattern Mining - 图53, then the actual frequency is 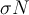Frequent Pattern Mining - 图54, and the frequency, 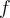Frequent Pattern Mining - 图55, on the frequency list should be at least Frequent Pattern Mining - 图56.
Thus if we output all of the items in the frequency list having 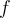Frequent Pattern Mining - 图57 value of at least 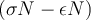Frequent Pattern Mining - 图58, then all of the frequent items will be output.
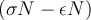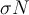In addition, some sub-frequent items will be output too (whose actual frequency is at least Frequent Pattern Mining - 图59 but less than Frequent Pattern Mining - 图60).