Multidimensional OLAP analysis is still needed in stream data analysis. 流数据分析仍然需要多维OLAP分析。
Due to the limited memory, disk space, and processing power, it is impossible to store the detailed level of data and compute a fully materialised cube 由于有限的内存、磁盘空间和处理能力,不可能存储详细级别的数据并计算完全物化的立方体
How can we implement Stream OLAP? Three key techniques for Stream OLAP:
- Tilted time frame 倾斜的时间框架
- Critical layer storing 关键层储存
- Partial materialisation 部分物化
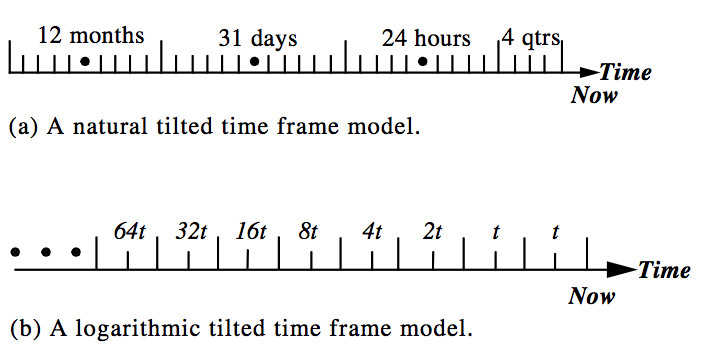
Tilted Time Frame: Time Dimension with Compressed Time Scale
- Key idea: The most recent time is registered at the finest granularity; the most distant time is registered at a coarser granularity. 最近的时间以最细的粒度记录,最遥远的时间以较粗粒度记录
- The level of coarseness desirable depends on applications. 期望的粗糙度水平取决于应用
- Two examples to design a tilted time frame:
- Natural tilted time frame model 自然倾斜时间模型
- Time frame is structured in multiple granularities based on the natural time scale (See example in the figure (a) below). 时间框架是基于自然时间尺度以多种粒度构建的
- Heading from now back in time, we store the most recent 4 quarter-hours, followed by the last 24 hours, then 31 days, and then 12 months = 71 units of time describing a year up to the current time point. 从现在回到过去,我们存储最近的4个季度,然后是最近的24小时,然后是31天,然后是12个月= 71个时间单位,描述了截至当前时间点的一年
- Compute frequent item sets
- in the last hour with the precision of a quarter of an hour or
- in the last day with the precision of an hour …etc
2. Logarithmic tilted time frame model (figure (b) below) 对数倾斜时间框架模型
- Time frame is structured in multiple granularities according to a logarithmic scale. 时间框架是按照对数标度以多种粒度构建的。
- Suppose the most recent slot holds the current quarter-hour 假设最近的时间段是当前的一刻钟
- The remaining slots are for the previous quarter-hour, the half hour before that (2 quarters), the hour before that (4 quarters) , 8 quarters, and so on, with the slot time-size growing at an exponential rate backwards in time. 剩余的时间段是前一刻钟、前半小时(2个季度)、前一小时(4个季度)、8个季度等等,时间段大小以指数速度向后增长。
ACTION: Consider whether the summary measures of such a model need to be distributive, algebraic, or holistic.
Critical Layers 关键层
- Even with the tilted time frame model, it can still be too costly to dynamically compute and store a materialized cube. 即使使用倾斜时间框架, 但是动态计算和储存实体化立方体的成本仍然太高
- Compute and store only some mission-critical cuboids of the full data cube 计算并储存完整数据立方体的一些关键任务立方体
- Dynamically and incrementally compute and store two critical cuboids (or layers)
- The first layer, called the minimal interest layer, is the minimally interesting layer that an analyst would like to study. 第一层称为最小兴趣层,是分析师希望研究的最小兴趣层。
- The second layer, called the observation layer, is the layer at which an analyst (or an automated system) would like to continuously study the data. 第二层称为观察层,是分析师(或自动化系统)希望持续研究数据的层。
- These layers are determined based on their conceptual and computational importance in stream data analysis 这些层是根据它们在流数据分析中的概念和计算重要性来确定的
Example of Critical Layers
- Dimensions at the raw data layer includes individual user, street address, and second.
- At the minimal interest layer, the three dimensions are user group, street block, and minute, respectively.
- Any cuboids that are lower than the minimal interest layer are beyond user interest.
- We only need to compute and store the (three-dimensional) aggregate cells for the (user group, street block, minute).
- At the observation layer, the three dimensions are ∗ (meaning all user), city, and quarter, respectively.
- The cuboids at the observation layer should be computed dynamically, taking the tilted time frame model into account as well.
- This is the layer that an analyst takes as an observation to make decisions.
Partial Materialisation
“What if a user needs a layer that would be between the two critical layers?”
Materialising a cube at only two critical layers leaves much room for how to compute the cuboids in between. These cuboids can be precomputed fully, partially, or not at all (i.e., leave everything to be computed on the fly).
Popular path cubing:
- rolls up the cuboids from the minimal interest layer to the observation layer by following one popular drilling path 沿着一条常见的钻孔路径,将立方体从最小兴趣层向上滚动到观察层
- materialises only the layers along the path, and leaves other layers to be computed only when needed. 仅将路径沿线的图层材料化,并仅在需要时才计算其他图层。

