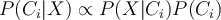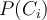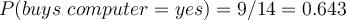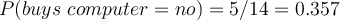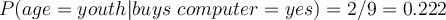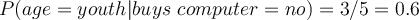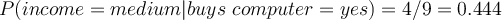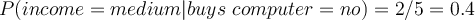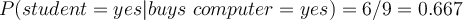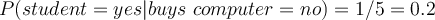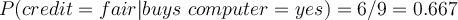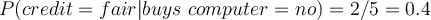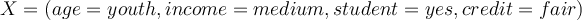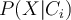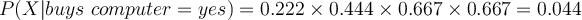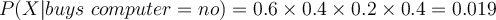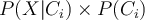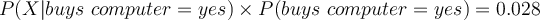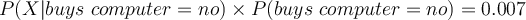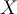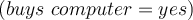Naive Bayes Classification method
- Let
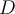 be a training set of tuples and their associated class labels, and each tuple is represented by an n-Dimensional attribute vector
be a training set of tuples and their associated class labels, and each tuple is represented by an n-Dimensional attribute vector 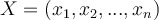
- Suppose there are
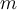 classes
classes 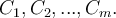
- Classification aims to derive the maximum posteriori, i.e., the maximal
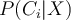 using Bayes’ theorem
using Bayes’ theorem 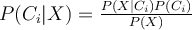
For Naive Bayes, we simplify Bayes’ theorem to reduce the computation cost of each likelihood in the training phase. Instead of a computing and recording a likelihood for each tuple for each class in our training set, we summarise by computing a likelihood for each attribute value for each class, that is, the class distribution for each attribute value. Statistically, we are making an assumption that, within each class, each attribute is independent of all the others.
Class conditional independence: We assume the object’s attribute values are conditionally independent of each other given a class label, so we can write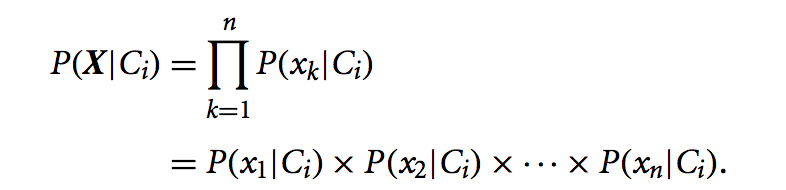
- In other words, we factorise each attribute in the likelihood function, by _assuming that there are no dependence relationships amongst the attribu_tes. 换句话说,我们通过假设属性之间没有依赖关系,来分解似然函数中的每个属性。
- This greatly reduces the computation cost as it only counts the class distribution 这大大降低了计算成本,因为它只计算类分布
- If
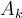 is categorical,
is categorical, 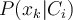 is the number of tuples in
is the number of tuples in 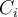 having value
having value 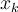 for
for 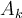 divided by
divided by 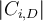 (number of tuples of
(number of tuples of 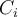 in
in 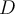 )
) - Blithely assuming class conditional independence of attributes is naive, hence the name of the method. It is not checked, and is commonly even known to be untrue, however, it seems to work, mostly.
Example
Let’s compute the likelihood of the previous example using the assumption of class conditional independence
| age | credit | buys_computer |
|---|---|---|
| youth | fair | no |
| youth | fair | yes |
| middle_aged | excellent | yes |
| middle_aged | fair | no |
| youth | excellent | no |
| middle_aged | excellent | no |
| middle_aged | fair | yes |
- With the conditional independence assumption, the likelihood of tuple (youth, excellent) is
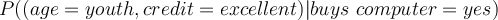
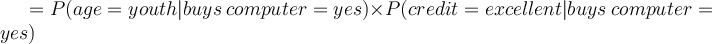
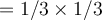
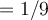
- We can also see here that we have mitigated the limitation observed earlier caused by the lack of observations for (youth, excellent) actually buying a computer.
Example 2
Here we have some more complex customer history with four different attributes. | age | income | student | credit | buys_computer | | —- | —- | —- | —- | —- | | youth | high | no | fair | no | | youth | high | no | excellent | no | | middle_aged | high | no | fair | yes | | senior | medium | no | fair | yes | | senior | low | yes | fair | yes | | senior | low | yes | excellent | no | | middle_aged | low | yes | excellent | yes | | youth | medium | no | fair | no | | youth | low | yes | fair | yes | | senior | medium | yes | fair | yes | | youth | medium | yes | excellent | yes | | middle_aged | medium | no | excellent | yes | | middle_aged | high | yes | fair | yes | | senior | medium | no | excellent | no |
- Compute conditional probability
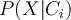 for each class
for each class
- Predict probability of
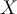 buying computer
buying computer