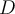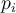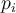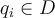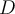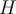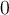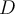Clustering tendency assessment determines whether a given data set has a non-random structure, which may lead to meaningful clusters.

    • Assess if non-random structure exists in the data by measuring the probability that the data is generated by a uniform data distribution
    • Test spatial randomness by statistical test: Hopkins Statistic 通过统计检验检验空间随机性:霍普金斯统计
      • Given a dataset 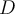Assessing Clustering Tendency - 图1 regarded as a sample of a random variable 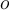Assessing Clustering Tendency - 图2, determine how far away Assessing Clustering Tendency - 图3 is from being uniformly distributed in the data space
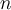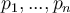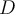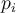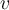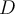
      • Sample Assessing Clustering Tendency - 图4 points, Assessing Clustering Tendency - 图5, uniformly from the range of Assessing Clustering Tendency - 图6. For each Assessing Clustering Tendency - 图7, find its nearest neighbour in Assessing Clustering Tendency - 图8 where Assessing Clustering Tendency - 图9 in Assessing Clustering Tendency - 图10
        • For example, if Assessing Clustering Tendency - 图11 consists of real valued observations whose minimum value is 0.5 and maximum value is 6.2, then Assessing Clustering Tendency - 图12 is a random value sampled uniformly between 0.5 and 6.2.
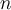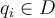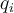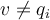
      • Sample Assessing Clustering Tendency - 图13 points, Assessing Clustering Tendency - 图14, uniformly from Assessing Clustering Tendency - 图15 (Assessing Clustering Tendency - 图16). For each Assessing Clustering Tendency - 图17, find its nearest neighbour in Assessing Clustering Tendency - 图18 where Assessing Clustering Tendency - 图19 in Assessing Clustering Tendency - 图20 and Assessing Clustering Tendency - 图21
        • Unlike Assessing Clustering Tendency - 图22, Assessing Clustering Tendency - 图23 is one of the existing values in Assessing Clustering Tendency - 图24 (i.e. Assessing Clustering Tendency - 图25).
      • Calculate the Hopkins Statistic:

    Assessing Clustering Tendency - 图26

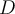    1.   - If [![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623665712782-c3075a9f-86e4-414b-8e71-f08872ac2aed.png#align=left&display=inline&height=14&margin=%5Bobject%20Object%5D&originHeight=14&originWidth=15&size=0&status=done&style=none&width=15)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=D) is uniformly distributed, [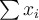![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623665712757-d659de5d-e498-4b7a-8006-a9f76853f3b9.png#align=left&display=inline&height=20&margin=%5Bobject%20Object%5D&originHeight=20&originWidth=39&size=0&status=done&style=none&width=39)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=%5Csum%20x_i) and [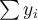![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623665712754-8623b6b3-f1d9-4ecf-ab36-2b5206819ec2.png#align=left&display=inline&height=20&margin=%5Bobject%20Object%5D&originHeight=20&originWidth=38&size=0&status=done&style=none&width=38)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=%5Csum%20y_i) will be close to each other and [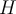![](https://cdn.nlark.com/yuque/0/2021/png/21710893/1623665712729-5ad6520d-de43-4f67-af80-38c027d57ce9.png#align=left&display=inline&height=14&margin=%5Bobject%20Object%5D&originHeight=14&originWidth=16&size=0&status=done&style=none&width=16)](https://wattlecourses.anu.edu.au/filter/tex/displaytex.php?texexp=H) is close to 0.5.
    • If Assessing Clustering Tendency - 图27 is highly skewed, Assessing Clustering Tendency - 图28 is c lose to Assessing Clustering Tendency - 图29
      • If Assessing Clustering Tendency - 图30 is uniformly distributed 均匀分布 then it contains no meaningful clusters.