Putting it together: Ranking in the vector space model

Example: ranking for information retrieval

1. Query: Weight query terms as TF-IDF
2. Documents: Weight document terms by TF

1. Compute 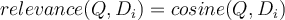(see cosine similarity)**
   That is, the relevance of document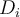 expressed as a TF-weighted vector, to the query expressed as a TF-IDF-weighted vector, is given by the cosine similarity of the vectors.

In the above, sometimes the Query and Document vectors are normalised in steps 1 and 2 respectively by dividing each element of the vector by length of the vector (also called the vector norm or Euclidean norm) , which is computed as the square-root of the sum of the square of each element (remember Pythagoras?). This will also ensure that each element in the normalised vector is on the interval [0,1]. Noting that in step 3 you the apply the cosine formula, which has a divisor that is the product of the lengths of the two vectors anyway, you did not strictly need to normalise them first to get the same result.

Example: Below we can see the Query and 3 documents, D, D and D _projected on to 2-D vector space (or where |v| =2, so only 2 dimensions). _D is the most relevant because the angle between Query and D is the smallest. Similarly, the ranking order will be D _D _D.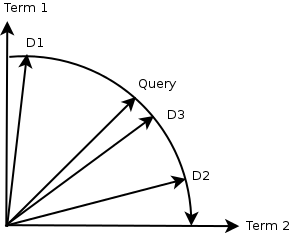

How do you know if your relevance ranking is any good?

• Carry out experiments using Precision, Recall or F-score, where you have a “gold standard“ set of validation queries with the “right” answers already selected by people.
• On-line learning from user behaviour and feedback can be used to improve performance: relevance feedback
• This is the underlying basis of modern web search, but there are many more things done, too.