In this section, we will see how to report the performance of the models by various methods.
Accuracy (or error rate) on training data is not a good indicator of future performance because the model may be overly-tuned towards exactly the data on which it was trained. For example, consider the model which internally simply remembers the data it has seen and classifies that data as it was classified in the training data, and every new data item is classified arbitrarily. Would you expect this model to work well?
This situation is called overfitting and commonly leads to poor performance on unseen data.
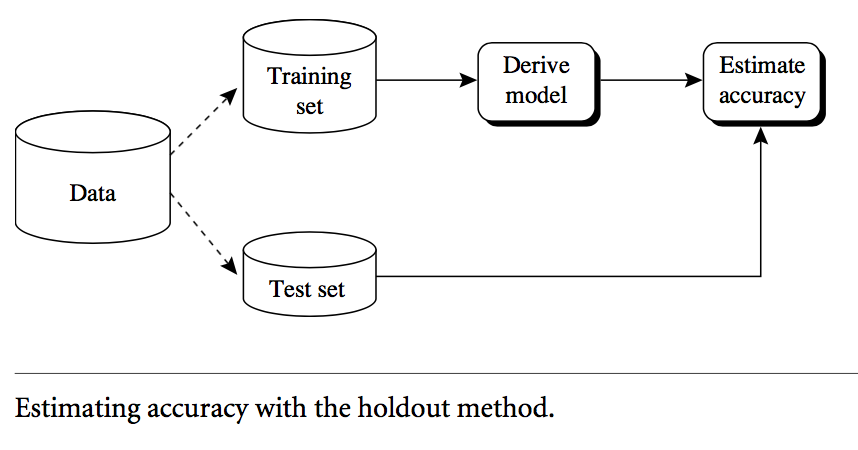
Holdout method**
- Given data is randomly partitioned into two independent sets
- Training set (e.g., 2/3) for model construction
- Test set (e.g., 1/3) for accuracy estimation
- Overall flow of holdout method:
Training / Validation / Test
- Randomly partition the given data into three different sets:
- Training set
- To construct (i.e train) a classification model
- Validation set
- To find the best parameters for the model, likely to be done by a person studying the effect of various parameters on the accuracy (or other quality measures) of the training set.
- To find the best parameters for the model, likely to be done by a person studying the effect of various parameters on the accuracy (or other quality measures) of the training set.
- Test set
- To measure the final performance of the model as it would be reported.
Cross-validation**
- k-fold, where k = 10 is most popular (due to low bias and variance)
- Randomly partition the data into k mutually exclusive subsets
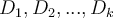 , each approximately equal size
, each approximately equal size - At i-th iteration, use
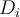 as test set and others as training set
as test set and others as training set - Leave-one-out: Special case for _small-sized dataset_s: Use k folds where k = number of tuples,
- Stratified cross-validation: Special case where folds are not randomly selected but stratified so that the class distribution in each fold is approximately the same as that in the initial data (to achieve low bias).
- Overall accuracy is computed as the average accuracy of each model on its respective test set.
Bootstrap
- Works well for small data sets where, otherwise, the requirement to split the data into training and testing sets makes both sets too small for purpose.
- Samples the given training tuples uniformly with replacement
- i.e., each time a tuple is selected, it is equally likely to be selected again and added to the training set again.
- i.e., each time a tuple is selected, it is equally likely to be selected again and added to the training set again.
- Several bootstrap methods : a common one is .632 bootstrap
- A data set with
 tuples is sampled
tuples is sampled 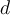 times, with replacement, resulting in a training set of
times, with replacement, resulting in a training set of 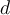 samples. The data tuples that did not make it into the training set end up forming the test set. About 63.2% of the original data end up in the training set, and the remaining 36.8% form the test set (since
samples. The data tuples that did not make it into the training set end up forming the test set. About 63.2% of the original data end up in the training set, and the remaining 36.8% form the test set (since 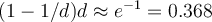 if
if 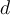 is very large.)
is very large.) - Repeat the sampling procedure
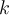 times, overall accuracy of the model is:
times, overall accuracy of the model is: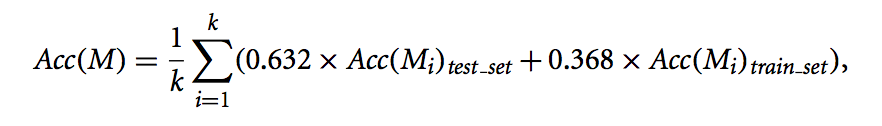
where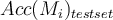 is the accuracy of the model trained with training set
is the accuracy of the model trained with training set 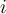 when it is applied to test set
when it is applied to test set 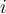 and
and 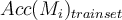 is the accuracy of the model obtained with training set
is the accuracy of the model obtained with training set 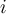 when it is applied to the training set
when it is applied to the training set 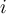 .
.
- A data set with

