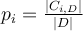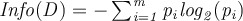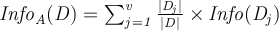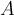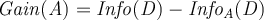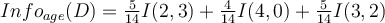Information Gain

    • This was a very early method that sprang from AI research in ID3, and was refined further to become Gain Ratio in C4.5.
    • It selects the attribute to split on with the highest information gain 选择信息增益最大的属性来拆分节点
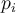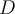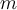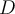    • Let Information Gain - 图1 be the probability that an arbitrary tuple in Information Gain - 图2 belongs to class Information Gain - 图3, of Information Gain - 图4 classes, where Information Gain - 图5 is the set of tuples in Information Gain - 图6 labelled with class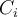 Information Gain - 图7
      • estimated by Information Gain - 图8 相对应的类别占节点总类别的比例
    • Expected information (entropy) needed to classify a tuple in 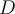Information Gain - 图9is defined by

    Information Gain - 图10

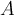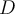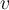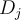    • After using attribute Information Gain - 图11 to split Information Gain - 图12 into Information Gain - 图13 partitions, corresponding to each attribute value for Information Gain - 图14 , each one of these partitions being Information Gain - 图15, the information that is still needed to separate the classes is:

    Information Gain - 图16

    • Therefore, information gained by branching on attribute Information Gain - 图17 is given by
      Information Gain - 图18

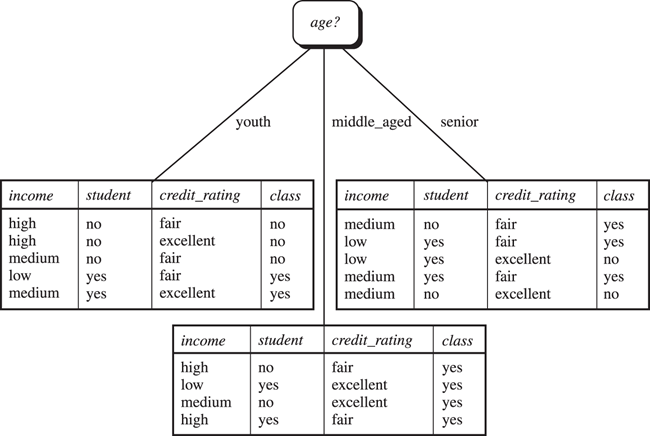
    Example (continued from previous)
    image.png

    Consider 2 classes: Class P is buyscomputer = “yes”. Class _N is buyscomputer = “no”
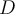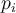    For some partition on Information Gain - 图20 with Information Gain - 图21 examples of _P     and 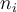Information Gain - 图22 examples of N, let 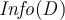Information Gain - 图23 be written as Information Gain - 图24.

    Using the definition 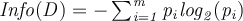Information Gain - 图25 from above,

    we have 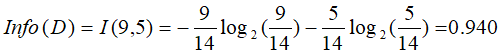image.png
    Now consider the first partition on _age. _We have the following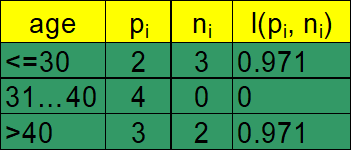
    image.png

    and so
    Information Gain - 图28
    = 0.694

    Therefore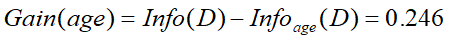
    image.png
    Similarly,
    image.png
    So Gain(age) is optimal and we split on age to get

    image.png