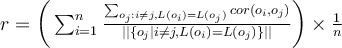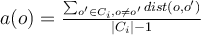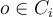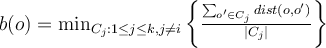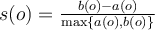• Two methods: extrinsic vs. intrinsic 外在 vs 内在
  • Extrinsic: supervised, i.e., the ground truth is available 外在的:受监督的，即有基本事实
    • Compare a clustering against the ground truth using certain clustering quality measure
    • Ex. BCubed precision and recall metrics 基于精确度和召回率的指标
  • Intrinsic: unsupervised, i.e., the ground truth is unavailable
    • Evaluate the goodness of a clustering by considering how well the clusters are separated, and how compact the clusters are
    • e.g. Silhouette coefficient below is objectively quantitative, but subjective judgement can be just as useful.

Extrinsic Methods
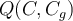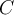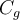To measure clustering quality, we need to define a score function Measure Clustering Quality - 图1 for a clustering Measure Clustering Quality - 图2 and a ground truth clusters Measure Clustering Quality - 图3.
Four criteria of a good score function:

  • Cluster homogeneity: The more pure the clusters, the better the clustering.
  • Cluster completeness: The couterpart of homogeneity. Any two objects belonging to the same category in the ground truth, should be assigned to the same cluster.
  • Rag bag: Rag bag category: objects that cannot be merged with other objects. Putting a heterogeneous object into a pure cluster should be penalised more than putting it into a rag bag.
  • Small cluster preservation: Splitting a small category into pieces is more harmful than splitting a large category into pieces.

BCubed precision and recall metrics satisfy the all four criteria.

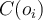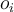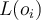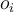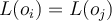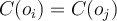  • Let Measure Clustering Quality - 图4 be the cluster number of object Measure Clustering Quality - 图5, Measure Clustering Quality - 图6 be the category of Measure Clustering Quality - 图7 given by the ground truth, and Measure Clustering Quality - 图8 be 1 if Measure Clustering Quality - 图9 and Measure Clustering Quality - 图10, otherwise 0.
  • BCubed precision: how many other objects in the same cluster belong to the same category as the object.

Measure Clustering Quality - 图11

  • BCubed recall: how many objects of the same category are assigned to the same cluster.

Measure Clustering Quality - 图12.

Intrinsic Methods

Two criteria for intrinsic method:

  • How well the clusters are separated
  • How compact the clusters are

1. Silhouette coefficient satisfies above two conditions.
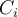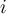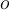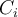Let Measure Clustering Quality - 图13 be the Measure Clustering Quality - 图14th cluster from a clustering and let Measure Clustering Quality - 图15 be an object in the cluster Measure Clustering Quality - 图16.

  • compactness, Measure Clustering Quality - 图17 where Measure Clustering Quality - 图18,
  • separation, Measure Clustering Quality - 图19

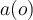Measure Clustering Quality - 图20 reflects the compactness of the cluster 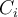Measure Clustering Quality - 图21, being the average distance of the object 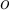Measure Clustering Quality - 图22 in the cluster from every other object in the cluster. Low compactness is good.
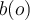Measure Clustering Quality - 图23 reflects the degree to which object 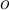Measure Clustering Quality - 图24 is separated from other clusters it does not belong to, being the average distance to all objects in the next-closest cluster. High separation is good.
The silhouette coefficient of 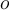Measure Clustering Quality - 图25 is then defined as:

  • Measure Clustering Quality - 图26.

The value lies between -1 and 1. A negative value means 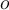Measure Clustering Quality - 图27 is closer to the objects in another cluster than to the objects in the same cluster in expectation, and this is normally undesirable.

To evaluate a particular cluster, average the silhouette coefficient for every object in the cluster. To evaluate a clustering, average the silhouette coefficient for every object in the dataset. Negative values are poor.
2. Visual inspection Plot the clusters (or a small random sample of the data instead of the whole dataset) in 2 dimensions (choose several pairs of dimensions for several plots, or choose pairs of dimensions that are expected to be important in the problem domain. You can plot in 3 dimensions if you prefer, but more than that and it gets very hard to inspect visually). Indicate the cluster membership by the colour coding of points on the plot. Do the clusters seem to be well separated and internally compact ?
3. Elbow method If you used the elbow method to choose an optimal number of clusters, was there a clear turning point in the plot, indicating that there is some inherent structural meaning to the k you chose?