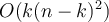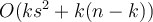Strength:

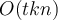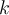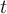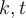  • Computationally Efficient: time complexity is Strength and Weakness - 图1, where Strength and Weakness - 图2 is the number of objects, Strength and Weakness - 图3 is the number of clusters, and Strength and Weakness - 图4 is the number of iterations. Normally, Strength and Weakness - 图5.
    • Comparing: PAM: Strength and Weakness - 图6, CLARA: Strength and Weakness - 图7

**

Weakness

  • Need to specify k, the number of clusters, in advance 需要提前去设定聚类的数目
  • Applicable only to objects in a continuous n-dimensional space 仅适用于连续n维空间中的对象
    • k-modes variant method for categorical data: replaces the mean value by the mode of a nominal attribute.
    • In comparison, k-medoids can be applied to a wide range of data k模型可以被运用到更大范围的数据
  • Sensitive to noisy data and outliers 对噪点数据和极值敏感。
  • Non deterministic algorithm. The final result depends on the first initialisation. 非确定性算法。最终结果取决于首次初始化。
  • Often terminates at a local optimum, rather than a global optimum. 经常终止在局部优化而不是全局最优。
  • Not suitable for clusters with non-convex shapes 不适用于非凸形状的簇


Noisy data point example

Consider six points in 1-D space having the values 1,2,3,8,9,10, and 25, respectively.
Intuitively, by visual inspection we may imagine the points partitioned into the clusters {1,2,3} and {8,9,10}, where point 25 is excluded because it appears to be an outlier. 直观地看，我们可以想象分成簇{1,2,3}和{8,9,10}的点，其中点25被排除，因为它看起来是一个离群值。
How would k-means partition the values? If we apply k-means using k = 2,

  • Case 1: partition values into {{1, 2, 3}, {8, 9, 10, 25}}. Within-cluster variation is
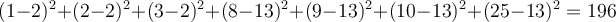    Strength and Weakness - 图8,
    given that the mean of cluster {1,2,3} is 2 and the mean of {8,9,10,25} is 13.
  • Case 2: partition values into {{1, 2, 3, 8}, {9, 10, 25}}. Within-cluster variation is
    Strength and Weakness - 图9,
    given that 3.5 is the mean of cluster {1, 2, 3, 8} and 14.67 is the mean of cluster {9, 10, 25}.

The latter partitioning has the lowest within-cluster variation; therefore, the k-means method assigns the value 8 to a cluster different from that containing 9 and 10 due to the outlier point 25. Moreover, the centre of the second cluster, 14.67, is substantially far from all the members in the cluster. 后一种划分具有最低的簇内变化；因此，由于离群点25，k-均值方法将值8分配给不同于包含9和10的聚类。此外，第二个集群的中心14.67基本上远离集群中的所有成员。