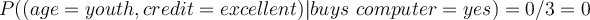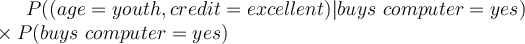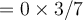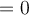In the following example, we would like to classify whether a certain customer would buy a computer or not. We have a customer purchase history as follows:
| age | credit | buys_computer |
|---|---|---|
| youth | fair | no |
| youth | fair | yes |
| middle_aged | excellent | yes |
| middle_aged | fair | no |
| youth | excellent | no |
| middle_aged | excellent | no |
| middle_aged | fair | yes |
What is the probability of (youth, excellent) customer buying a computer?
- If we compute the likelihood
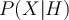 :As we can see, we observe 0 likelihood for buying a computer with attribute (age=youth, credit=excellent).
:As we can see, we observe 0 likelihood for buying a computer with attribute (age=youth, credit=excellent).
- Therefore, posterior probability of tuples with (age=youth, credit=excellent) will be 0:
- This does not mean that every buyer with (age=youth, credit=excellent) would not buy a computer.
- The data contains some information about customers who are youth or have excellent credit.
- But the classifier ignores it because there are no who are youth and have excellent credit.
- It is usual to interpret this to mean that the number of observations is too small to obtain a reliable posterior probability.
- This tendency toward having zero probability will increase as we incorporate more and more attributes.
- Because we need at least one observation for every possible combination of attributes and target classes.
- Because we need at least one observation for every possible combination of attributes and target classes.
- In the next section, we will see that this problem is mitigated somewhat with naive Bayes that assumes class conditional independence, but we will still need the Laplacian correction when there is some attribute value which has not been seen in some class in the training data.