1. 定义:
蒙特卡洛分析(又称:模拟):在定量风险分析中,使用蒙特卡洛分析来模拟单个项目风险和其他不确定性来源的综合影响,以评估它们对项目目标的潜在影响。
- 对成本风险进行蒙特卡洛分析时,使用项目成本估算作为模拟的输入;
对进度风险进行蒙特卡洛分析时,使用进度网络图和持续时间估算作为模拟的输入。
开展综合定量成本/进度风险分析时,同时使用这两种输入。其输出就是定量风险分析模型。用计算机软件数千次迭代运行定量风险分析模型。每次运行,都要随机选择输入值(如成本估算、持续时间估算或概率分支发生频率)。这些运行的输出构成了项目可能结果(如项目结束日期、项目完工成本)的区间。典型的输出包括:表示模拟得到特定结果的次数的直方图,或表示获得等于或小于特定数值的结果的累积概率分布曲线(S 曲线)。蒙特卡洛成本风险分析所得到的 S 曲线示例
模拟是采用蒙特卡洛分析法,把单个项目风险和不确定性的其他来源模型化的方法,以评估它们对项目目标的潜在影响。它利用风险和其他不确定资源计算整个项目可能的进度结果。模拟包括基于多种不同的活动假设、制约因素、风险、问题或情景,使用概率分布和不确定性的其他表现形式来计算出多种可能的工作包持续时间。上图显示了一个项目的概率分布,表明实现特定目标总持续时间的可能性
2. 蒙特卡洛分析:持续时间估算概率分布
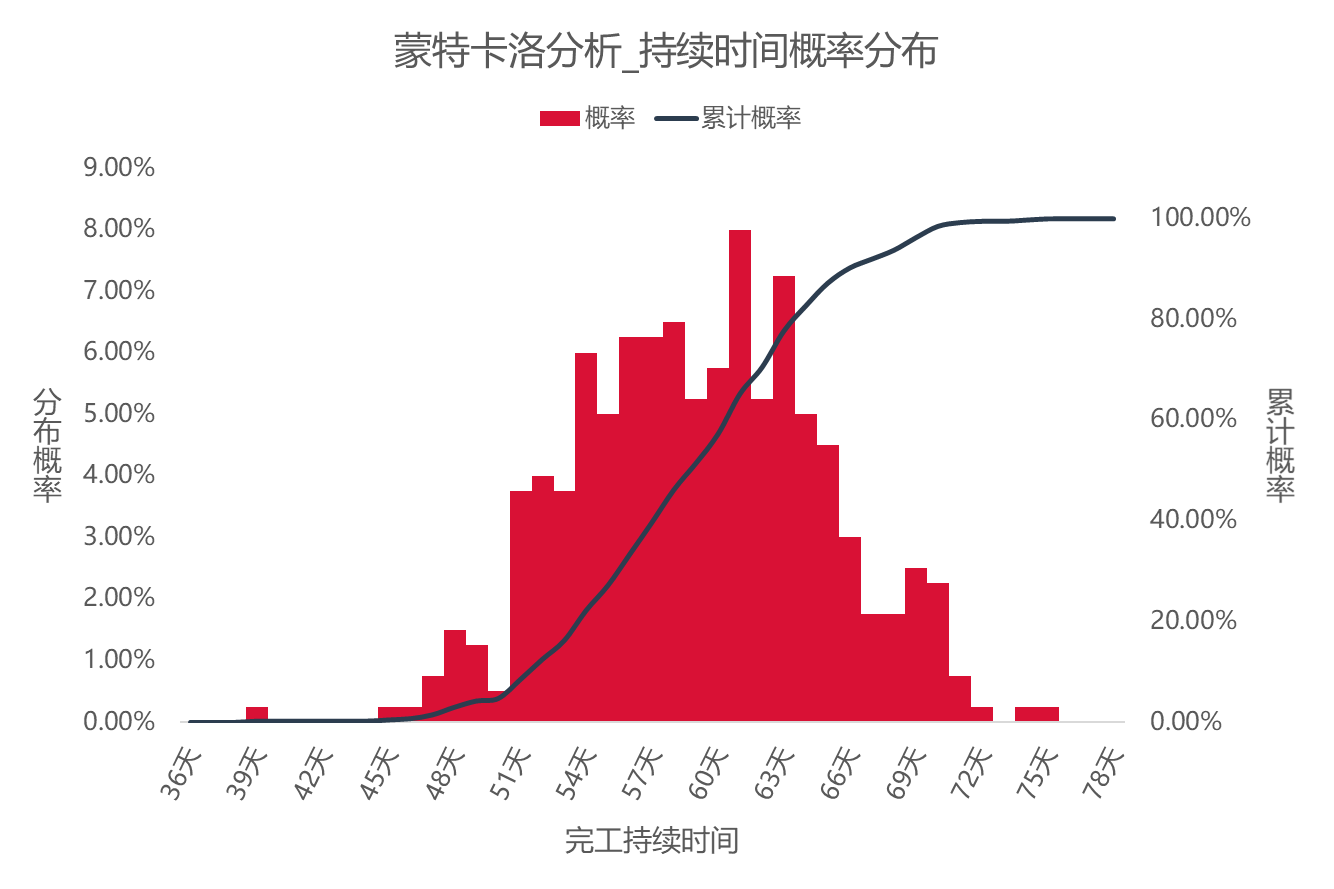
X轴:持续时间,单位为天
- Y轴左侧:为红色直方图的分布概率,表示:假设的完成项目目标所需要的天数所发生的的概率
- Y轴右侧:为蓝色S曲线的累计概率,表示:随着天数往后推移,最终累积概率能出现接近100%的情况
- 启示:随着时间不断往后推移,项目目标是必定100%完成。即是说,一个任务假如需要5天来完成,那么给予10天,给予20天的话,是肯定100%能完成。但这完全是浪费,模拟数据分析的目的在于,分析完成项目目标的把握(概率)。如上图,如果客户只给55天要求完成项目,那么从图上能找到对应的累计概率是37%,这样概率比较低,把握不是太高,就没必冒险向客户承诺;但是如果给到63天,那么累积概率就去到80%,能够完成目标的概率就大有把握。
当然,最终决策是采用多少天,还需要综合经济考量、相关方的利益、以及其他相关的因素。蒙特卡洛分析是帮我我们从量化概率的角度,去观察完成一个项目目标的把握程度
3. 蒙特卡洛分析:成本估算概率分布 S曲线

X轴:完工成本,单位为货币
- Y轴:为蓝色S曲线的累计概率,表示:随着所给予成本,能够完成项目的累计概率
- 启示:随着成本不断增加,项目目标是必定100%完成。即是说,一个项目需要6000元完成,那么给予10000元,甚至给予15000元的话,是肯定100%能完成。但这完全是浪费,模拟数据分析的目的在于,分析完成项目目标的把握(概率)。如上图,如果项目只给5200元要求完成项目,那么从图上能找到对应的累计概率是8%,这样概率比非常低,根本就是冒险;但是如果给到6500元,那么累积概率就去到80%,能够完成目标的概率就大有把握。
- 显示该项目以5200元完成的可能性是8% 。如果组织比较保守,想要有80%的成功可能性,那就需要把预算定位6500元(约包括25%=[ (6500元-5200元/ 5200元]的应急储备)
4. 如何进行蒙特卡洛分析
- 确定分析对象,输入和输出的数据分别是那些
- 建模,确定服从那种分布概率模型(正态分布、β分布、三角分布),用Excel来构建数据表格和图表
- 输入数以千计的随机数,产生图表
- 根据目标问题,分析图表,
- 生成结论(需要重新定位预算或者工期、增加多少应急储备等等)

