定义:
- CPM是项目总工期最长的路径,从时间范围跨度来说。
- CPM也是项目最短的工期,即最早能完成项目的时间
- 目的:在项目进度模型中,估算项目最短工期,确定逻辑网络路径的进度灵活性大小的一种方法。
名词解释:
| ES | Early Start Date | 最早开始日期 | 某进度活动未完部分可能开始的最早时点。 | | —- | —- | —- | —- | | EF | Early Finish Date | 最早完成日期 | 某进度活动未完部分可能完成的最早时点。 | | LS | Late Start Date | 最晚开始日期 | 进度活动未完成部分可能的最晚开始时点。 | | LF | Late Finish Date | 最晚完成日期 | 进度活动未完成部分可能的最晚完成时点。 | | TF | Total Float | 总浮动时间 | 指一项活动不影响总工期的机动时间
总浮动时间可能是正值、零或负值 | | FF | Free Float | 自由浮动时间 | 指一项活动不影响后续活动工期的机动时间 |
七格法(6标时法,英国标准BS6046所标识的节点)
| ES | DU | EF |
|---|---|---|
| Activity ID | ||
| LS | TF | LF |
| 最早开始 | 持续时间 | 最早结束 |
|---|---|---|
| 活动ID | ||
| 最晚开始 | 总浮动时差 | 最晚结束 |
★★特别注意
- 如果我们说具体到“几月几号”到“几月几号”,请务必用数数的方式来确认,中间有多少天存在。
- 如果我们说具体到“第几天”到“第几天”,请务必用数数的方式来确认,中间有多少天存在。
- 如果前置任务A从第一天开始,执行了五天,那么后置任务B,开始执行天数是:第六天
- 特别注意,是否存在“早上8点”,这些字眼,统计绩效是统计这一天的之前那些日子的绩效(题目非常阴险)
- 特别注意,工作任务是否仅限于工作日,周一至周五,周六日不计算 :::
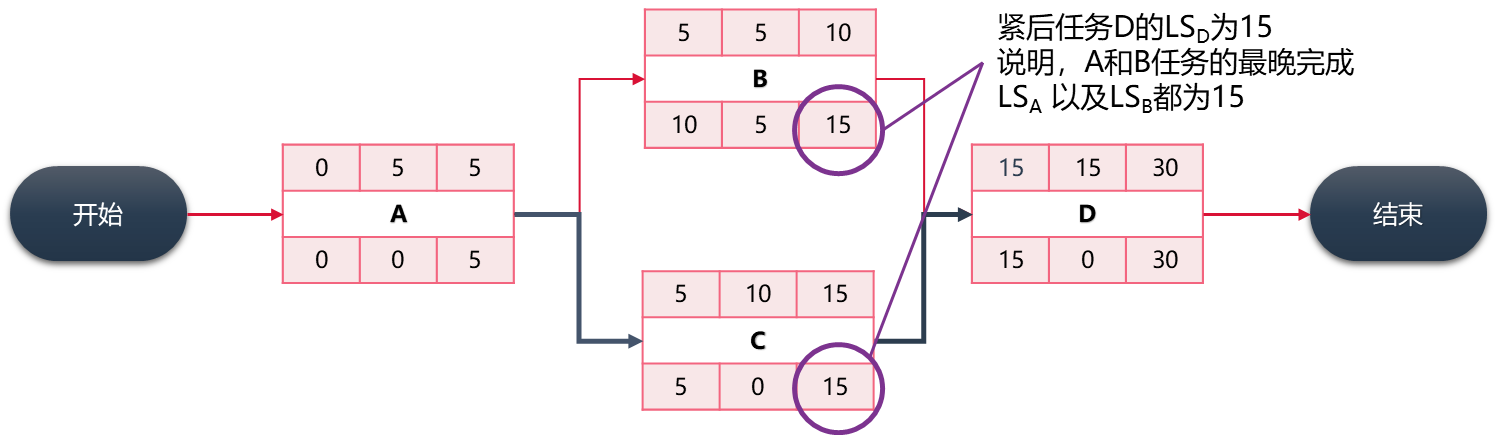
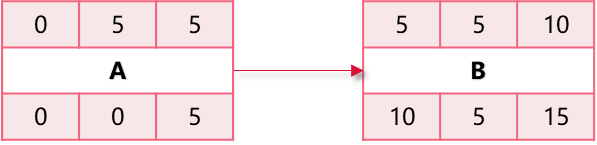
第一个活动的ES,设置为“第0天”的场合:
公式:
- 活动时间:DU = EF – ES
- 最早完成时间:EF = DU + ES
总时差 Total Float(总浮动):
定义:一项工作不影响总工期的前提,具有的机动时间
TF = LS - ES = LF - EF自由时差 Free Float(自由浮动):
定义:一项工作不影响紧后工作的前提,具有的机动时间
FF = 紧后活动的 ES - 紧前活动 EF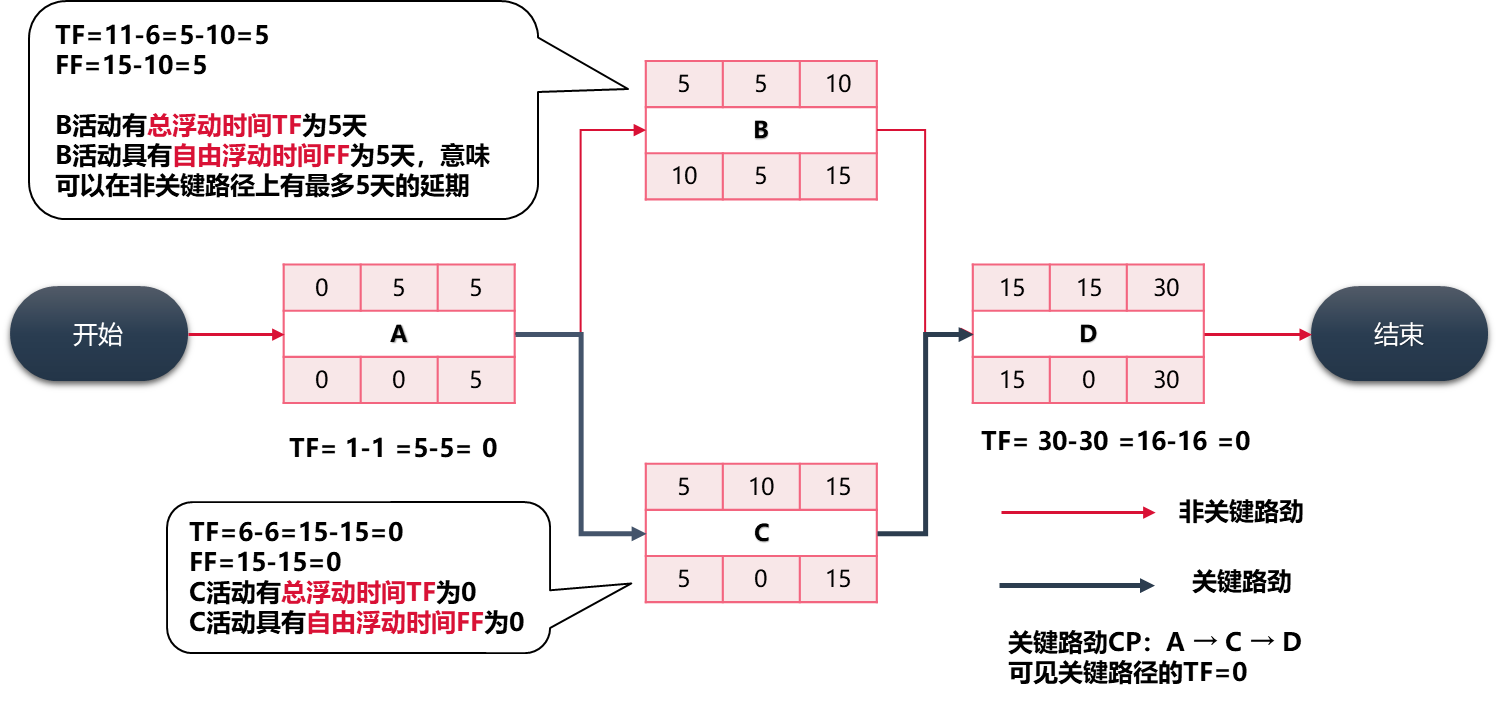
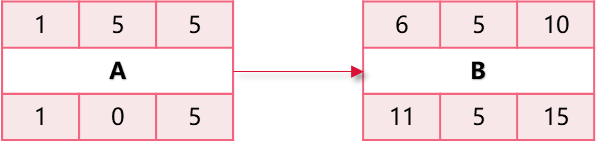
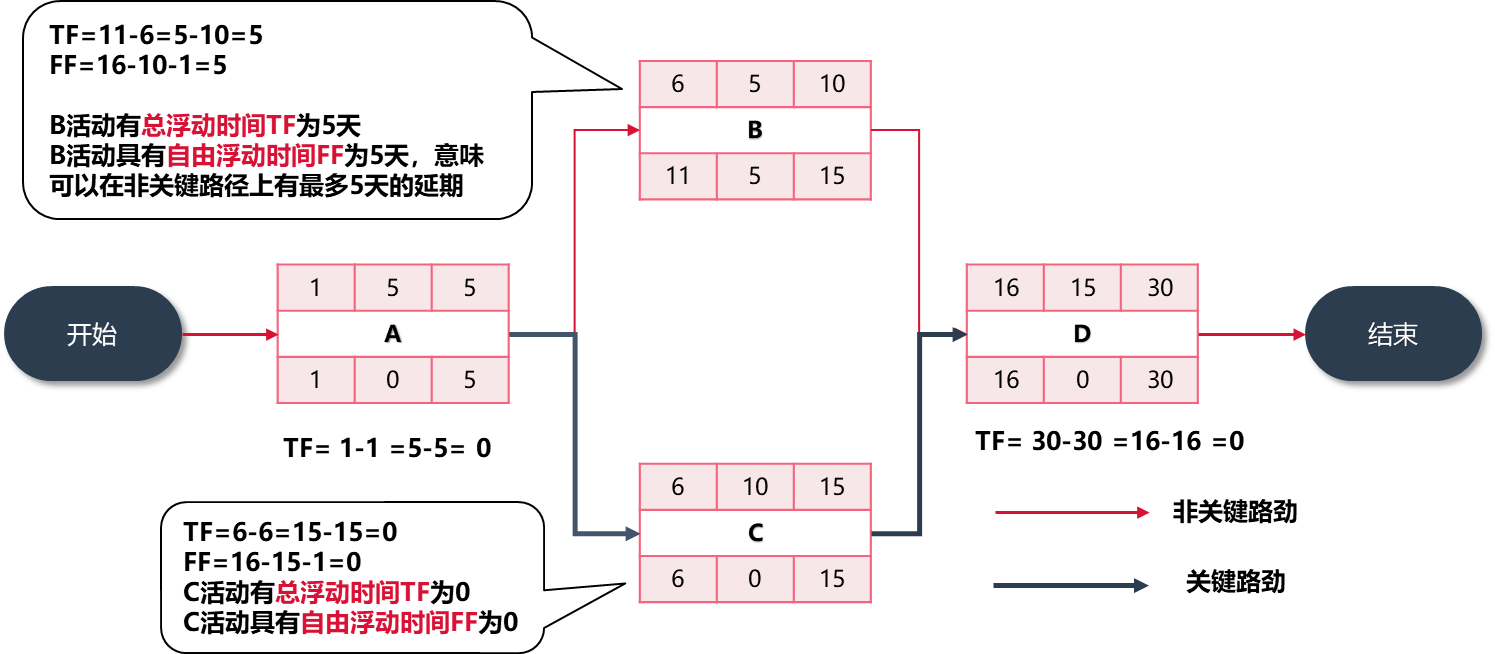
第一个活动的ES,设置为“第1天”的场合:
公式:
- 活动时间:DU = EF – ES + 1
- 最早完成时间:EF = DU + ES - 1
总时差 Total Float(总浮动):
定义:一项工作不影响总工期的前提,具有的机动时间
TF = LS - ES = LF - EF自由时差 Free Float(自由浮动):
定义:一项工作不影响紧后工作的前提,具有的机动时间
FF = 紧后活动的 ES - 紧前活动 EF - 1
★★★CPM的注意事项★★★:
- CPM前提是:不考虑资源制约的条件,理想化活动的先后顺序以及持续时间。
- CPM核心思想:增加项目的灵活性。总浮动TF越大,越灵活,但要注意不要超过客户的日期要求。
- CP(Critical Path)是项目总工期最长的路径。
- CP(Critical Path)也是项目顺利地完成的最短的工期,即最早完成的项目时间。
- 一个项目至少一条CP,可以有多条CP
- CP越多,项目风险越高
- 关键路径是可以随时发生变化(变为非关键路径),非关键路径也有可能转变为关键路径
- 次关键路径(Near-Critical Path),这是比CPM稍短的一条路径(仅次于CP),同时它制约CP可以压缩的时间。言下之意,当希望对CP原本10天工期压缩到7天,但是,存在一条Near CP的工期为8天。因此对CP而言,最多只能压缩至8天。与此同时,8天工期Near CP也会变成新的CP,因此就有两条关键路径。
- 非关键路径的最后一个非关键活动,存在自由浮动时间TF
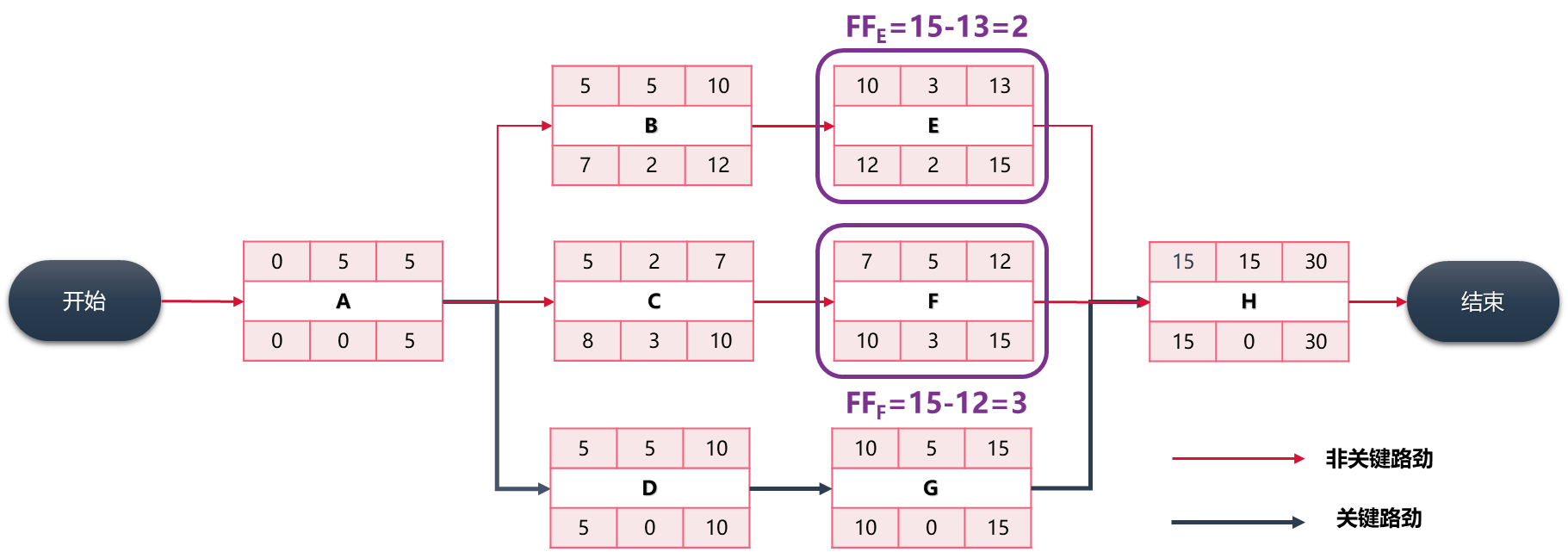
上图中:
- E活动的自由时差:FF**E**=15-13=2天
- F活动的自由时差:FF**F**=15-12=3天
- 其他非关键路径的总浮动时间TF,等于关键路径总时间减去此非关键路径的总时间
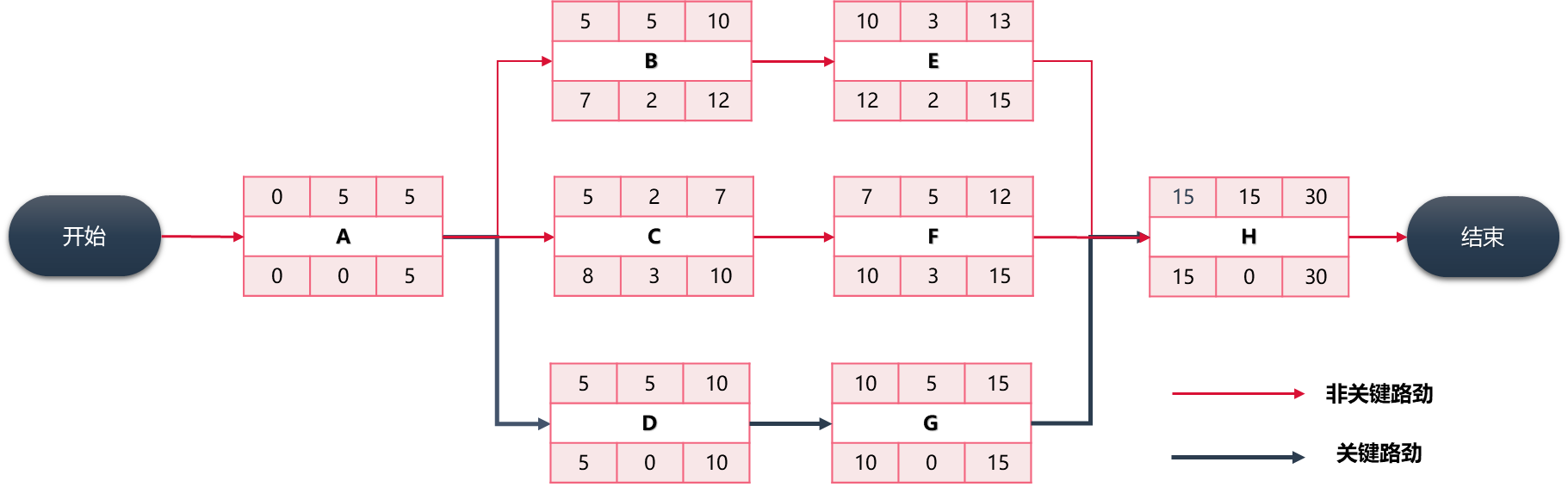
- 非关键路径ABEH:Non-CPBE = 28天
- 非关键路径ACFH:Non-CPCF = 27天
- 关键路径ADGH:CPADGH = 30天
- 总时差TTBE= CPADGH - Non-CPBE = 30 - 28 = 2天
- 总时差TTCF= CPADGH - Non-CPCF = 30 - 27 = 3天
- 非关键路径的所有活动都具有相同的的TT,因此TTBE = TTB = TTE= 2天;TTCF =TTC = TTF = 3天
- 在进行紧前关系绘图法排序的过程中,取决于所用的制约因素,关键路径的TF可能是正值、零或负值。
- 正常情况下,CP上的 TF=0 和 FF=0。上图中的TT**ADGH**=0
- 正常情况下,当开始活动或结束活动,有且仅有一个时,那么它(它们)必定属于CP。
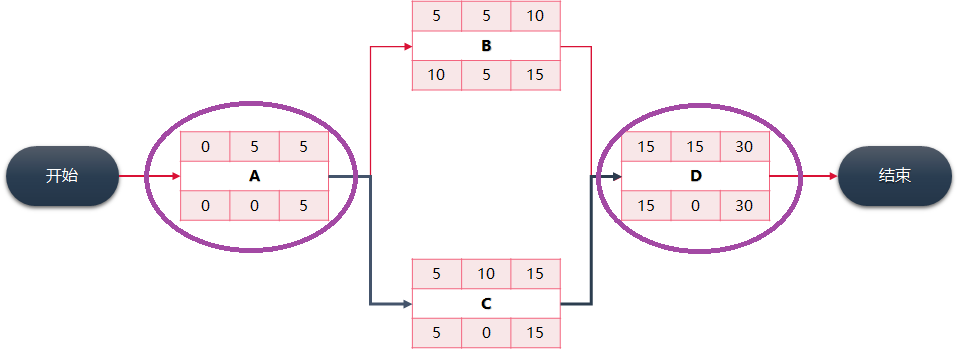
- 求最早完成时间用正推法,最晚开始时间用倒推法,下方底部有详细说明
- 当TF为正值,由于逆推计算所得的最晚完成日期晚于(大于)顺推计算所得出的最早完成日期,如下图
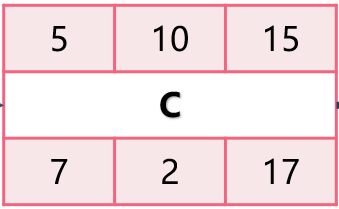
- 当TF为负值,顺推的最早完工时间晚于(大于)客户要求的完工时间,当用逆推法仍然使用客户要求的完工时间计算,就会发生TF为负值(负总时差)。
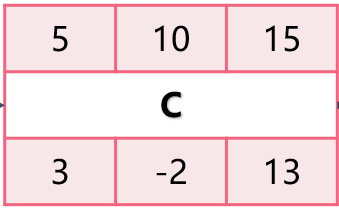
- 造成TF为负值原因:①客户或管理层要求比原定计划提前完工;②关键路径上的活动被延误; 对任何一个事件,负时差都预示着需要立即采取纠正措施,以满足客户对完工日期的要求。
- 负值浮动时间分析是一种有助于找到推动延迟的进度回到正轨的方法的技木。
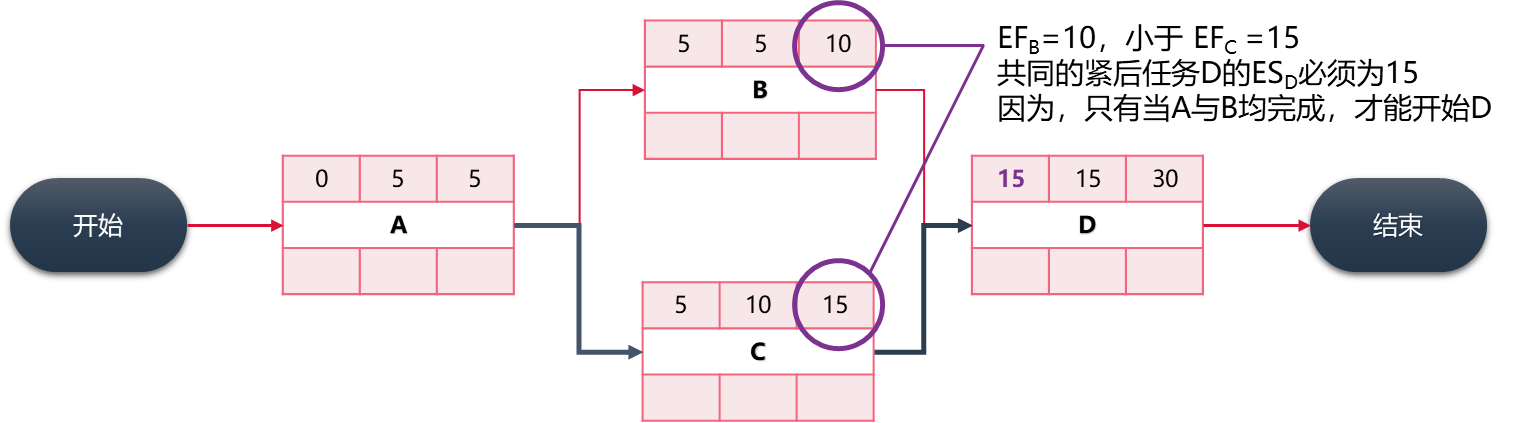
关于正推法和倒推法
正推法
倒推法