字符串匹配经典算法

算法背景

字符串匹配的目的是在主串S中匹配模式串P，并返回匹配结果（S中匹配子串的起始下标）。
最直接的方法就是暴力循环两个字符串，该方法时间复杂度为O(mn)，算法较为耗时。
为了降低算法的时间复杂度，对匹配方法做出优化，并最终实现了在时间复杂度O(m+n)下的快速字符串匹配，即KMP算法。

算法解析

算法思想

对正常匹配过程进行分析，当匹配进行到主串的位置i，模式串的位置j处发生了失配，如图所示。那么意味着，主串的[i-j:i]与模式串的[0:j]是完全匹配的。那么，能否从完全匹配的部分中寻找优化的可能性，来加速匹配是KMP的关键思想。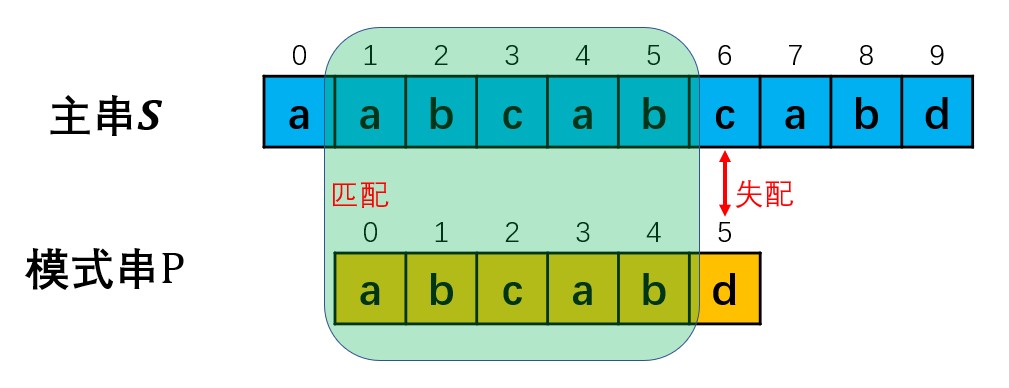

在暴力解法中，发生失配后会将模式串向后移动一位继续匹配。但是我们可以发现，已经匹配的部分中，主串中末尾部分与模式串中的开头部分相同。也就是说，只有将模式串前端的0,1位于主串的4,5位对齐，才有可能在后续的匹配中实现完全匹配。此时我们一次性的将模式串移动了三位，相比于暴力解法大大提升了匹配速度。
为了方便确定每次需要将模式串移动的位数，这里引入KMP算法的精髓——next数组。

next数组

next数组中记录了模式串中的字串[0:j]中，前缀与后缀相等的元素个数。以下通过几个例子进行说明。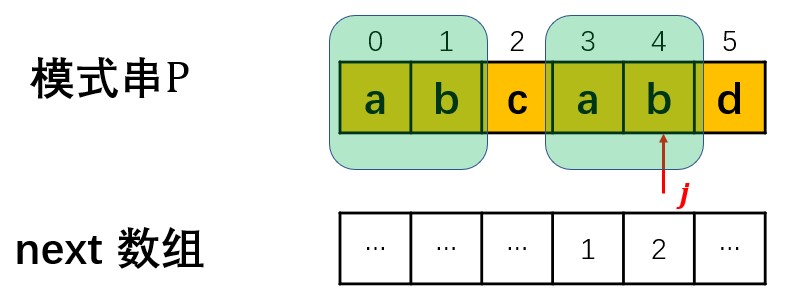

对于子串[0:4]前缀[0:1]与后缀[3:4]相同，因此next[4]的值为2。借助next数组便可以实现模式串的快速移动。
然而如何求解next数组呢？
不难发现，求取next数组便是模式串与自身匹配的过程。next[0]默认为0，匹配从第一位开始。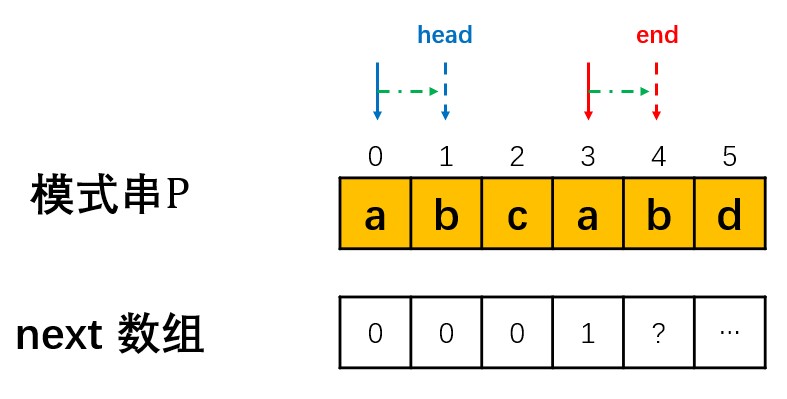

首先设置两个指针head和end分别表示前缀的最后一位和后缀的最后一位（当前匹配位）用于匹配。对于p[head]=p[end]的情况，假设此时end=4且匹配在end=3处的结果为1，即head[0]与end[3]匹配。这时将两个指针向后移一位，若此时head与end依然匹配，则next[end] = next[end-1]+1，随后继续将head和end向后移动。
对于p[head]!=p[end]的情况，则需要运用递归的思路进行处理，如下图所示。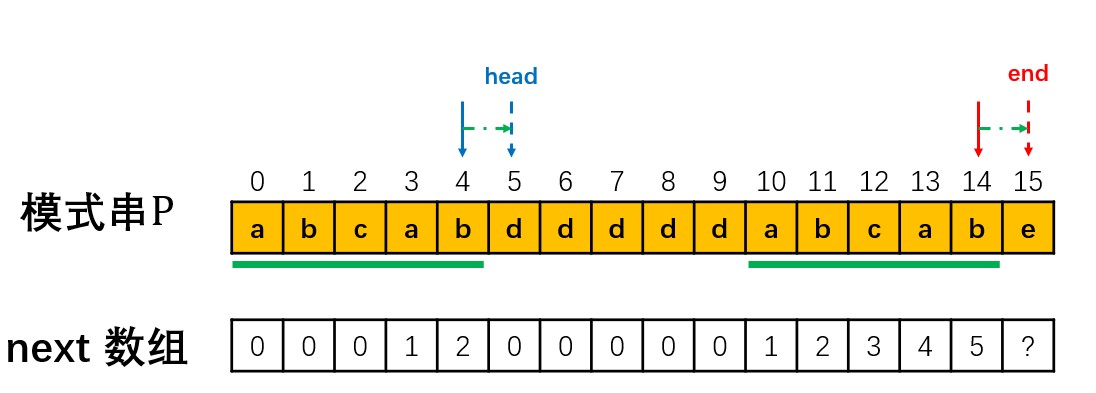

此时需要将head左移至head_new，在保证左右两个绿色底线的子串最大重叠的情况下继续匹配，即p[0:head_new-1]=p[end-head_new:end-1]。不难发现，这里便用到了先前生成的next数组。通过next[head-1]=2可知，将head移动至head_new = next[head-1]=2处可以获得最大重叠并继续匹配。
随后对head_new=2与end=15进行对比，若此时p[15]='c'，则p[head_new]=p[end]，通过相等时的方式进行处理。然而此时p[head_new]!=p[end]，继续两者不相等的处理办法，此时head_new被更新到了位置0。对于该种特殊情况，表示[0:end]的子串中没有相同的前缀和后缀，因此设置next[end]=0，并将next移动至下一位继续比较。
上述方法通过C++实现如下所示。

vector<int> GetNext(string p) {
        vector<int> next;
        int i = 0;        // 匹配的前缀
        int j = 1;        // 匹配的后缀
        next.push_back(0);        // next[0] 默认为0
        while (j<p.size()) {
            if(p[i]==p[j]) {
                i++;
                next.push_back(i);
                j++;
            }
            else {
                if(i==0) {
                    next.push_back(i);
                    j++;
                }
                else {
                    i = next[i-1];
                }
            }
        }
        return next;
    }

KMP字符匹配

随后便可以利用next数组进行字符匹配，这里需要三个指针进行匹配。
指针i表示主串S中匹配进行到的位置，i的取值范围为[0, s.size()-1]当i进行到s.size()处依旧没有完成匹配时，认为主串中不包含模式串。
指针j表示模式串P中匹配进行到的位置，j的取值范围为[0, p.size()-1]，当j进行到p.size()处时，表明匹配已经完成，此时返回主串中包含的模式串的首位指针即可。
指针pos表示主串中匹配开始的位置，即匹配成功后需要返回的值，pos的取值范围为[0:s.size()-p.size()]，超出此范围便认为匹配失败。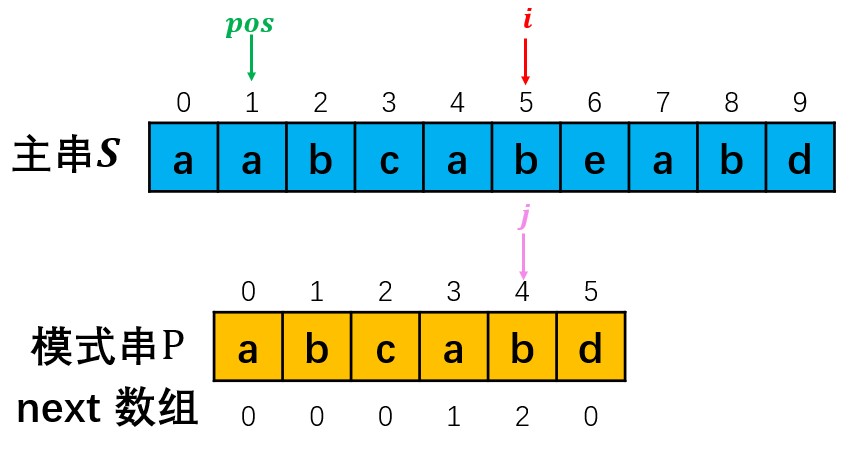

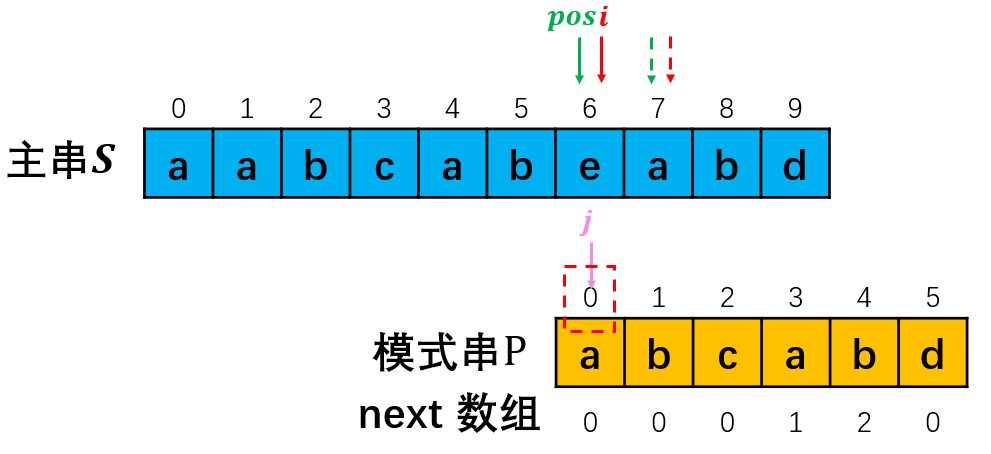
在匹配过程中，若p[i]==p[j]则将i, j后移一位，对下一位进行匹配。（如下图所示）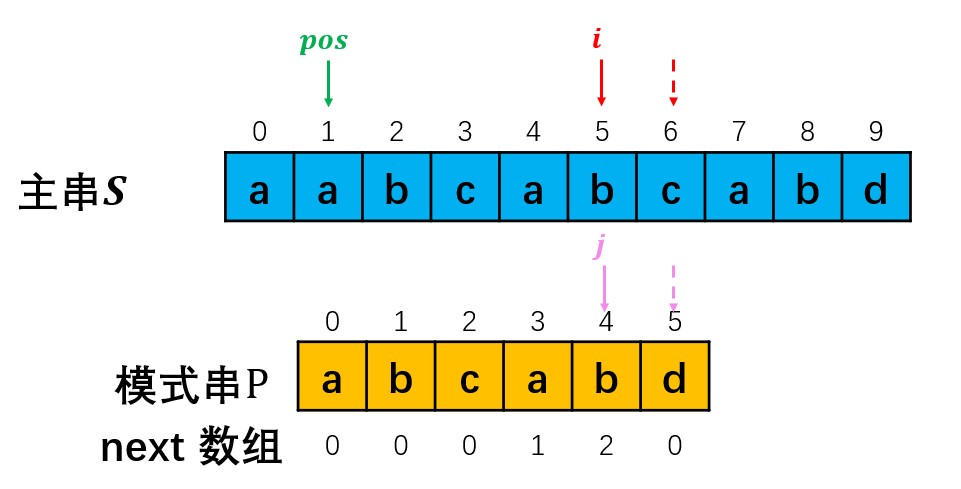

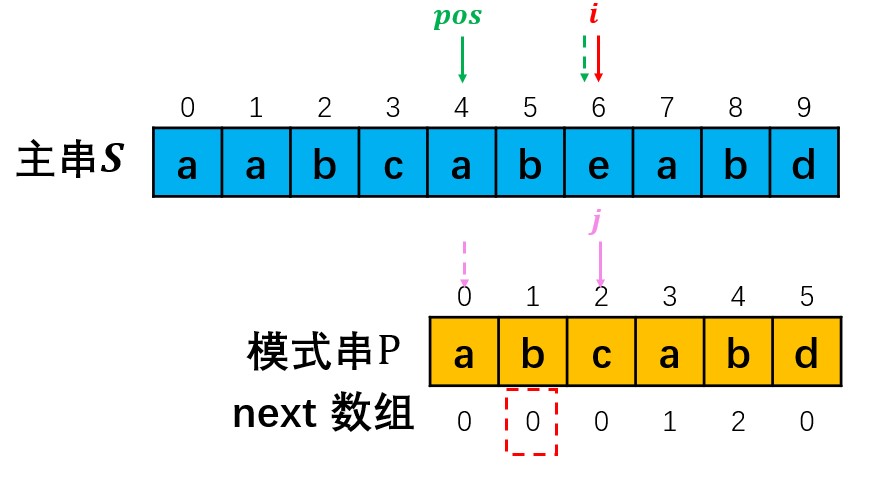
若p[i]!=p[j]时，若此时j>0，则需要根据next数组移动模式串，具体为pos = pos + (j - next[j-1])，并将指针j移动至next[j-1]处；若此时j==0，则需要同时将pos和i向后移动一位，重新开始匹配。（如下图所示）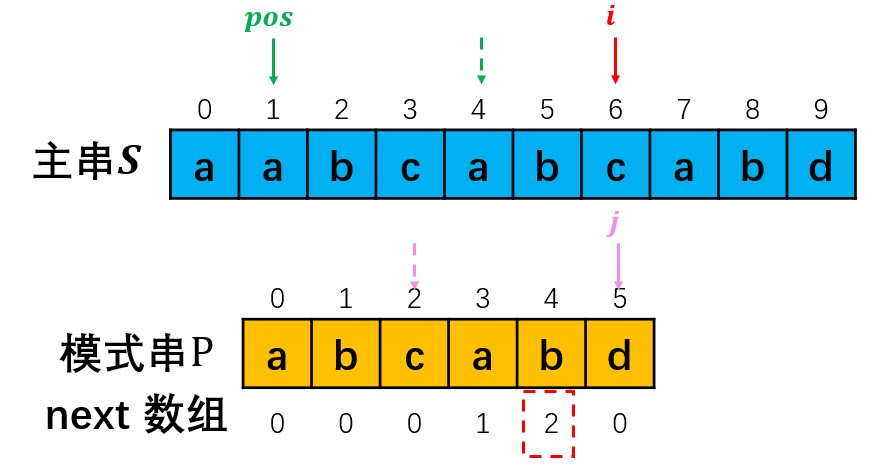

KMP算法的C++实现

#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
using namespace std;
class Solution {
private:
    vector<int> GetNext(string p) {
        vector<int> next;
        int i = 0;
        int j = 1;
        next.push_back(0);
        while (j<p.size()) {
            if(p[i]==p[j]) {
                i++;
                next.push_back(i);
                j++;
            }
            else {
                if(i==0) {
                    next.push_back(i);
                    j++;
                }
                else {
                    i = next[i-1];
                }
            }
        }
        return next;
    }
public:
    int search_KMP(string s, string p) {
        int n_s = s.size();
        int n_p = p.size();
        if (n_p>n_s)    return -1;
        vector<int> next = GetNext(p);
        int i = 0;
        int j = 0;
        int pos = 0;
        while (i<n_s && pos<=n_s-n_p) {
            if(s[i]==p[j]) {
                i++;
                j++;
            }
            else {
                if (j>0) {
                    pos += j - next[j-1];
                    j = next[j-1];
                }
                else {
                    pos++;
                    i++;
                }
            }
            if (j==n_p) return pos;
        }
        return -1;
    }
};
int main () {
    string p = "abcabcdab";
    string s = "abeabcabcdab";
    Solution solution;
    int result = solution.search_KMP(s, p);
    cout << "pos:" << result << endl;
    return 0;
}

LeetCode