题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4

题目数据保证输入的树是 完全二叉树

解题方法

递归遍历

递归计算二叉树节点数目，递归终止条件是当前节点为NULL，此时返回0，否则返回 左子树节点数+右子树节点数+1
时间复杂的O(n)，空间复杂度O(logn)
C++代码：

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  int countNodes(TreeNode* root) {
      if(!root)   return 0;
      int left = countNodes(root->left);
      int right = countNodes(root->right);
      return left + right + 1;
  }
};

迭代

BFS 层序遍历，记录总结点数目。
时间复杂度O(n)，空间复杂度额O(n)
C++代码：

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  int countNodes(TreeNode* root) {
      queue<TreeNode*> nodes;
      int num = 0;
      if(root)   nodes.push(root);
      while(nodes.size()>0) {
          int size = nodes.size();
          for(int i=0; i<size; i++) {
              num++;
              if(nodes.front()->left)     nodes.push(nodes.front()->left);
              if(nodes.front()->right)    nodes.push(nodes.front()->right);
              nodes.pop();
          }
      }

      return num;
  }
};

二分查找

根据完全二叉树的性质，可以判断当前节点左右子树的完全二叉树深度，从而更新查找方向。根据节点索引规律更新节点数目。
时间复杂度O((logn)^2)，空间复杂度O(1)
C++代码：

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  int check(TreeNode *cur) {
      if(!cur)    return 0;
      int num = 1;
      while(cur) {
          if(cur->left && cur->right) num++;
          cur = cur->right;
      }
      return num;
  }

  int countNodes(TreeNode* root) {
      if(!root) return 0;
      TreeNode *cur = root;
      int num = 1;

      while(cur) {
          if(check(cur->left)>check(cur->right)) {
              cur = cur->right;
              num = 2*num+1;
          }
          else {
              cur = cur->left;
              num = 2*num;
          }
      }

      return num-1;
  }
};

二分查找+位运算

根据完全二叉树定义，低层元素索引在[2^h, 2^(h+1)-1]中，在该范围内通过二分查找，判断对应索引的元素是否存在。
索引对应元素的查找通过位运算进行。索引按位由高到低，若是1则代表右节点，若为0则代表左节点。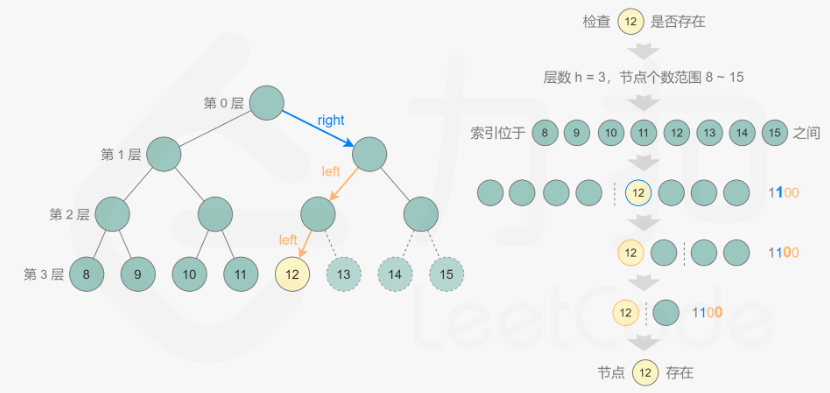

时间复杂度O((logn)^2)，空间复杂度O(1)
C++代码：

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  bool exits(TreeNode *root, int level, int k) {
      int bit = 1<<(level-1);
      TreeNode* cur = root;
      while(cur && bit>0) {
          if(k&bit)   cur = cur->right;
          else cur = cur->left;
          bit = bit>>1;
      }

      return cur!=NULL;
  }

  int countNodes(TreeNode* root) {
      if(!root) return 0;
      TreeNode *cur = root;
      int level = 0;
      while(cur->left) {
          level++;
          cur = cur->left;
      }

      int low = 1<<level;
      int high = (1<<(level+1))-1;
      while(low<high) {
          int mid = low + (high-low+1)/2;
          if(exits(root, level, mid)) low = mid;
          else    high = mid-1;
      }

      return low;
  }
};

LeetCode

222. 完全二叉树的节点个数

题目

解题方法

递归遍历

迭代

二分查找

二分查找+位运算