题目

给你两棵二叉树： root1 和root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：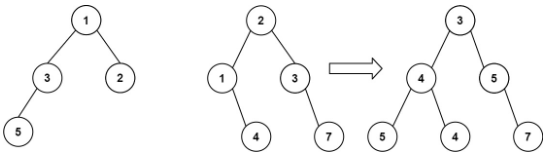
image.png

  1. 输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
  2. 输出：[3,4,5,5,4,null,7]

示例 2：

  1. 输入：root1 = [1], root2 = [1,2]
  2. 输出：[2,2]

提示：

  • 两棵树中的节点数目在范围 [0, 2000] 内

  • -10^4 <= Node.val <= 10^4

    解题方法

    DFS

    通过深度优先搜索判断各子节点，若两者都存在则合并，若有一个不存在，则返回存在的子节点。
    时间复杂度O(min(m,n))，空间复杂度O(min(m,n))
    C++代码：

    1. /**
    2. * Definition for a binary tree node.
    3. * struct TreeNode {
    4. *     int val;
    5. *     TreeNode *left;
    6. *     TreeNode *right;
    7. *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
    8. *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    9. *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
    10. * };
    11. */
    12. class Solution {
    13. public:
    14.   TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
    15.       if(root1==NULL && root2==NULL)  return NULL;
    16.       if(root1==NULL) return root2;
    17.       if(root2==NULL) return root1;
    18.       TreeNode* root = new TreeNode(root1->val + root2->val);
    19.       root->left = mergeTrees(root1->left, root2->left);
    20.       root->right = mergeTrees(root1->right, root2->right);
    22.       return root;
    23.   }
    24. };

    BFS

    层序遍历的方式，使用队列处理二叉树。
    时间复杂度O(min(m,n))，空间复杂度O(min(m,n))
    C++代码：

    1. /**
    2. * Definition for a binary tree node.
    3. * struct TreeNode {
    4. *     int val;
    5. *     TreeNode *left;
    6. *     TreeNode *right;
    7. *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
    8. *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    9. *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
    10. * };
    11. */
    12. class Solution {
    13. public:
    14.   TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
    15.       if(root1==NULL && root2==NULL)  return NULL;
    16.       if(root1==NULL) return root2;
    17.       if(root2==NULL) return root1;
    18.       TreeNode* root = new TreeNode(root1->val + root2->val);
    20.       queue<TreeNode*> tree1, tree2, tree;
    21.       tree.push(root);
    22.       tree1.push(root1);
    23.       tree2.push(root2);
    24.       while(!tree1.empty() && !tree2.empty()) {
    25.           TreeNode* node = tree.front();
    26.           TreeNode* node1 = tree1.front();
    27.           TreeNode* node2 = tree2.front();
    28.           tree.pop(); tree1.pop(); tree2.pop();
    29.           if(node1->left || node2->left) {
    30.               if(node1->left && node2->left) {
    31.                   node->left = new TreeNode(node1->left->val + node2->left->val);
    32.                   tree.push(node->left);
    33.                   tree1.push(node1->left);
    34.                   tree2.push(node2->left);
    35.               }
    36.               else if(node1->left)   node->left = node1->left;
    37.               else if(node2->left)   node->left = node2->left;
    38.           }
    39.           if(node1->right || node2->right) {
    40.               if(node1->right && node2->right) {
    41.                   node->right = new TreeNode(node1->right->val + node2->right->val);
    42.                   tree.push(node->right);
    43.                   tree1.push(node1->right);
    44.                   tree2.push(node2->right);
    45.               }
    46.               else if(node1->right)   node->right = node1->right;
    47.               else if(node2->right)   node->right = node2->right;
    48.           }
    49.       }
    51.       return root;
    52.   }
    53. };