题目

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

  1. 创建一个根节点，其值为 `nums` 中的最大值。
  1. 递归地在最大值 **左边** 的 **子数组前缀上** 构建左子树。
  1. 递归地在最大值 **右边** 的 **子数组后缀上** 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：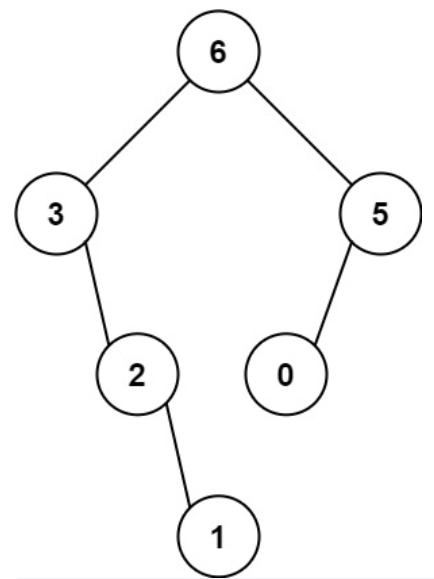

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：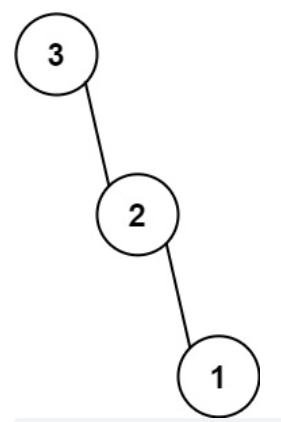

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数互不相同

解题方法

迭代+单调栈

采用单调递减栈存储未处理的节点，从左向右遍历数组，连续元素u和v存在如下关系：

u>v，v存在于u的右子树中
u<v，u存在于v的左子树中

具体流程如下：

  1. 从左向右遍历数组元素
     1. 若该元素小于栈顶元素，则该元素入栈。
     1. 若该元素大于栈顶元素，栈顶节点出栈，从上向下处理栈中小于该元素的节点
        1. 出栈元素作为栈顶元素右子树，并将该栈顶元素出栈，直到栈为空，或新栈顶元素大于数组当前元素。
        1. 将出栈元素作为数组当前元素的左子树
        1. 数组当前元素入栈
  2. 处理栈中剩余元素，直至栈中仅存根节点。

时间复杂度O(n)，空间复杂度O(n)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        int size = nums.size();
        if(!size)   return NULL;
        stack<TreeNode*> nodes;
        TreeNode* root = new TreeNode(nums[0]);
        nodes.push(root);
        for(int i=1; i<size; i++) {
            TreeNode* node = nodes.top();
            if(nums[i]<node->val) {
                TreeNode* tmp = new TreeNode(nums[i]);
                nodes.push(tmp);
            }
            else {
                nodes.pop();
                while(!nodes.empty() && nodes.top()->val<nums[i]) {
                    nodes.top()->right = node;
                    node = nodes.top();
                    nodes.pop();
                }
                TreeNode* tmp = new TreeNode(nums[i]);
                tmp->left = node;
                nodes.push(tmp);
            }
        }
        while(nodes.size()>1) {
            TreeNode* node = nodes.top();
            nodes.pop();
            nodes.top()->right = node;
        }

        return nodes.top();
    }
};

递归分治

按照题目思路，每次寻找数组最大值，在分别处理左右子数组。
时间复杂度O(n^2)（平均O(nlogn)最坏O(n^2)），空间复杂度O(n)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* MBT(vector<int>& nums, int left, int right) {
        if(left>right)  return NULL;
        if(left==right) return new TreeNode(nums[left]);
        int max_idx = left;
        for(int i=left; i<=right; i++) {
            if(nums[i]>nums[max_idx])   max_idx = i;
        }
        TreeNode* root = new TreeNode(nums[max_idx]);
        root->left = MBT(nums, left, max_idx-1);
        root->right = MBT(nums, max_idx+1, right);

        return root;
    }

    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        int size = nums.size();
        if(!size)   return NULL;

        return MBT(nums, 0, size-1);
    }
};

LeetCode

654. 最大二叉树

题目

解题方法

迭代+单调栈

递归分治