题目

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：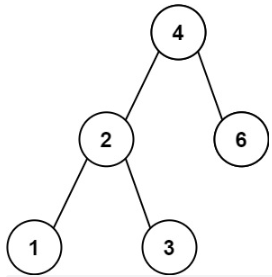
image.png

  1. 输入：root = [4,2,6,1,3]
  2. 输出：1

示例 2：
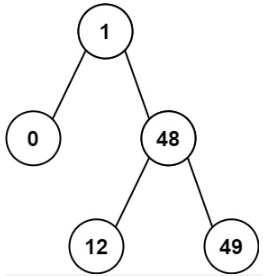
image.png

输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

  • 树中节点的数目范围是 [2, 10^4]

  • 0 <= Node.val <= 10^5

    解题方法

    递归

    采用递归中序遍历，记录并更新上一个元素以及最小绝对差。
    时间复杂度O(n)，空间复杂度O(n)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  void dfs(TreeNode* cur, int& last, int& mingap) {
      if(cur->left)   dfs(cur->left, last, mingap);
      mingap = mingap<(cur->val-last) ? mingap : (cur->val-last);
      last = cur->val;
      if(cur->right)  dfs(cur->right, last, mingap);
  }

  int getMinimumDifference(TreeNode* root) {
      int last = -10e5;
      int mingap = INT_MAX;
      dfs(root, last, mingap);
      return mingap;
  }
};

    Morris 中序遍历

    Morris 遍历降低空间复杂度
    时间复杂度O(n)，空间复杂度O(1)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  int getMinimumDifference(TreeNode* root) {
      int last = -10e5;
      int mingap = INT_MAX;
      TreeNode* cur = root;
      TreeNode* mostright;

      while(cur) {
          mostright = cur->left;
          if(mostright) {
              while(mostright->right && mostright->right!=cur)    mostright = mostright->right;
              if(!mostright->right) {
                  mostright->right = cur;
                  cur = cur->left;
              }
              else {
                  mostright->right = NULL;
                  mingap = mingap<(cur->val-last) ? mingap : (cur->val-last);
                  last = cur->val;
                  cur = cur->right;
              }
          }
          else {
              mingap = mingap<(cur->val-last) ? mingap : (cur->val-last);
              last = cur->val;
              cur = cur->right;
          }
      }
      return mingap;
  }
};