题目
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1: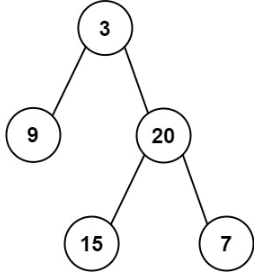
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历-
解题方法
递归+哈希表
通过哈希表重构中序遍历数组,方便对父节点下标的快速查找。通过递归的方式,先从后序数组的最后一位获取父节点,再根据哈希表对中序数组进行分割,再分别构建左右子树。
时间复杂度O(n),空间复杂度O(n)
C++代码:/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { private: map<int, int> map_in; public: TreeNode* mid_post(vector<int>& in, vector<int>& post, int in_left, int in_right, int post_left, int post_right) { if(in_left>in_right) return NULL; int mid = post[post_right]; TreeNode* root = new TreeNode(mid); int idx = map_in[mid]; int left_size = idx-in_left; root->left = mid_post(in, post, in_left, idx-1, post_left, post_left+left_size-1); root->right = mid_post(in, post, idx+1, in_right, post_left+left_size, post_right-1); return root; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { int size = inorder.size(); for(int i = 0; i<size; i++) { map_in[inorder[i]] = i; } return mid_post(inorder, postorder, 0, size-1, 0, size-1); } };迭代
效仿从前序和中序遍历恢复二叉树的方法,反向遍历后序数组及中序数组,后序数组中相邻元素
u和v只有两种可能:u是v的右节点u是v或其祖先节点的左节点
采用栈维护 未考虑过左节点 的节点。
该方法时间复杂度O(n),空间复杂度O(n)
C++代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int size = inorder.size();
if(!size) return NULL;
stack<TreeNode*> nodes;
TreeNode* root = new TreeNode(postorder[size-1]);
nodes.push(root);
int in_idx = size-1;
for(int i=size-2; i>=0; i--) {
TreeNode* node = nodes.top();
if(node->val != inorder[in_idx]) {
node->right = new TreeNode(postorder[i]);
nodes.push(node->right);
}
else {
while(!nodes.empty() && nodes.top()->val == inorder[in_idx]) {
node = nodes.top();
nodes.pop();
in_idx--;
}
node->left = new TreeNode(postorder[i]);
nodes.push(node->left);
}
}
return root;
}
};

