题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：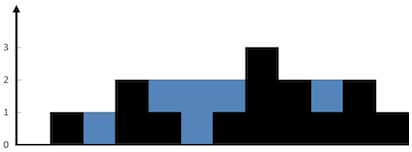
image.png

  1. 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
  2. 输出：6
  3. 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

  1. 输入：height = [4,2,0,3,2,5]
  2. 输出：9

提示：

  • n == height.length
  • 1 <= n <= 2 * 10^4

  • 0 <= height[i] <= 10^5

    解题方法

    动态规划

    每一列能够接的雨水量有该列左右两侧的最大值的较小值决定，因此可以预处理处每一列对应的左侧和右侧最大值，进而计算该列能够承接的雨水量。
    时间复杂度O(n)，空间复杂度O(n)。
    C++代码：

    1. class Solution {
    2. public:
    3.   int trap(vector<int>& height) {
    4.       int size = height.size();
    5.       vector<int> rest(size, INT_MAX);
    6.       int lmax = height[0], rmax = height[size-1];
    7.       for(int i=0; i<size; i++) {
    8.           lmax = lmax > height[i] ? lmax : height[i];
    9.           rmax = rmax > height[size-1-i] ? rmax : height[size-1-i];
    10.           rest[i] = rest[i] < lmax ? rest[i] : lmax;
    11.           rest[size-1-i] = rest[size-1-i] < rmax ? rest[size-1-i] : rmax;
    12.       }
    13.       int result = 0;
    14.       for(int i=0; i<size; i++) {
    15.           result += (rest[i]-height[i]);
    16.       }
    18.       return result;
    19.   }
    20. };

    单调栈

    使用递增单调栈保存递减序列，当寻找到下一个更大元素时，弹出当前元素，并根据前一个元素对当前元素所在位置进行雨水填充。
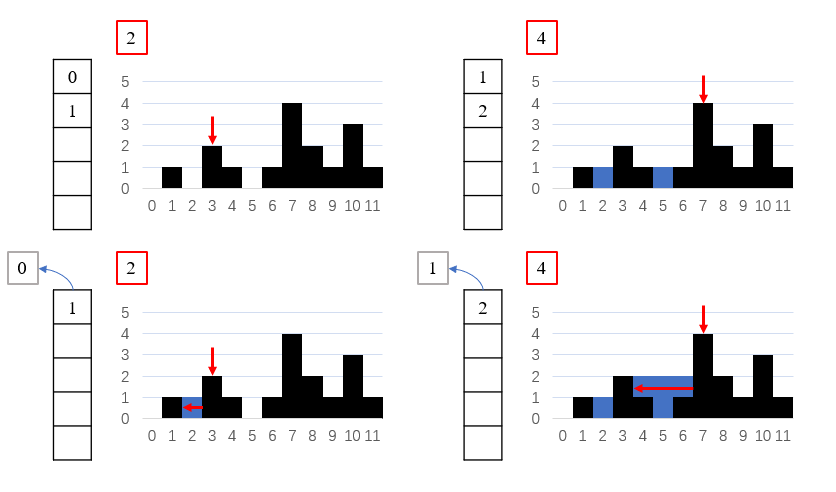
    image.png
    时间复杂度O(n)，空间复杂度O(n)。
    C++代码：

    class Solution {
public:
  int trap(vector<int>& height) {
      int size = height.size();
      stack<int> st;
      int result = 0;
      for(int i=0; i<size; i++) {
          while(!st.empty() && height[i]>height[st.top()]) {
              int mid = height[st.top()];
              st.pop();
              if(!st.empty()) {
                  result += (min(height[i], height[st.top()])-mid) * (i-st.top()-1);
              }
          }
          st.push(i);
      }

      return result;
  }
};

    双指针

    左右指针分别从左端和右端向中间移动，过程中维护左侧最大值与右侧最大值，通过height[left]和height[right]决定填充以及指针移动：

    • 如果height[left]<height[right]，则对于left处的元素必有lmax<lmax，故通过lmax填充left处，并将left右移。
    • 如果height[left]≥height[right]，则对于right处的元素必有lmax≥rmax，通过rmax填充right处，并将right左移

时间复杂度O(n)，空间复杂度O(1)。
C++代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int result = 0;
        int left = 0;
        int right = height.size()-1;
        int lmax = 0;
        int rmax = 0;
        while(left<right) {
            lmax = max(height[left], lmax);
            rmax = max(height[right], rmax);
            if(height[left]<height[right]) {
                result += lmax-height[left];
                left++;
            }
            else {
                result += rmax-height[right];
                right--;
            }
        }

        return result;
    }
};