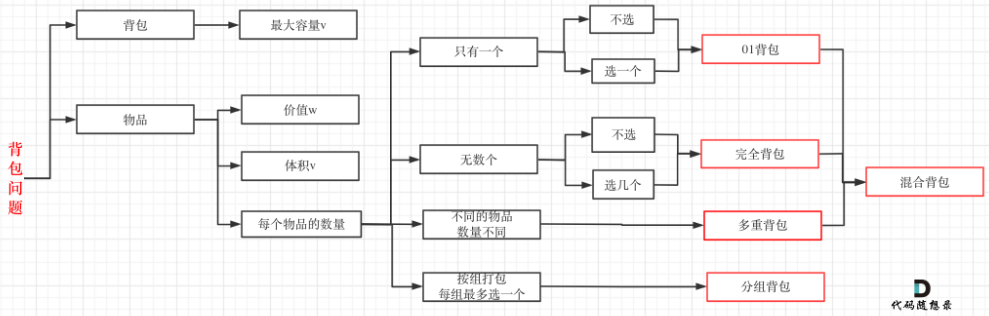
背包问题分类
问题描述
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
例:背包最大重量为4,物品如下:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
解题方法
二维动态数组
构建二维数组dp[i][j]表示从下标为[0-i]的物品中任取,放进容量为j的背包,价值总和最大为多少。
递推关系如下:
- 不放物品
i:由dp[i-1][j]推出,此时有dp[i][j] = dp[i-1][j] - 放物品
i:由dp[i-1][j-weight[i]]推出dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i](物品i的价值),就是背包放物品i得到的最大价值
所以递归公式为:
递推公式初始化:
- 当
j = 0时,背包无法放下任何物品,故价值总和一定为0; - 当
i = 0时,即要在各容量的背包中放下物品0,则有dp[0][j] = 0 (j<weight[0])以及dp[0][j] = value[0] (j≥weight[0])。
完整代码如下:
void bag() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;vector<vector<int>> dp(weight.size(), vector<int>(bagweight+1, 0));for(int j=weight[0]; j<=bagweight; j++) {dp[0][j] = value[0];}for(int i=1; i<weight.size(); i++) {for(int j=1; j<=bagweight; j++) {if(j<weight[i]) dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}return;}
一维动态数组
对于二维动态数组,如果采取行遍历的方式,可以通过一维数组进行优化,即dp[i]。
与二维动态数组不同的是,一维动态数组需要反向遍历,放置同一物品多次放置。
具体代码如下:
void bag() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;vector<int> dp(bagweight+1, 0);for(int i=weight[0]; i<=bagweight; i++) {dp[i] = value[0];}for(int i=1; i<weight.size(); i++) {for(int j=bagweight; j>=weight[i]; j--) {dp[j] = max(dp[j], dp[j-weight[i]] + value[i]);}}return;}