题目

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：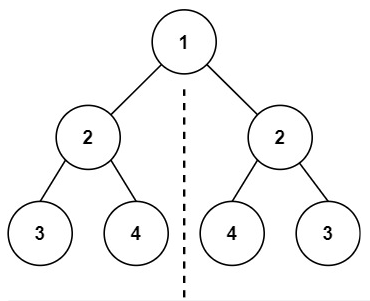

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：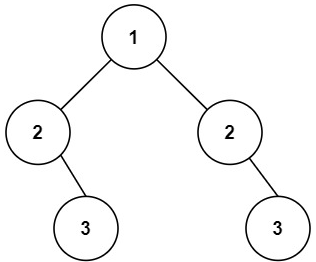

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

解题方法

关键点在于左右子树反向移动进行遍历。

递归

设置两个指针，从左右子树同时反向移动，遍历左右子树。对每个节点，若节点均不存在则认为对称；若节点均存在且值相等，判断该节点的左右子树，最终返回时候对称。其他情况则不对称。
时间复杂度O(n)，空间复杂度O(n)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool check(TreeNode* left, TreeNode* right) {
        if(!left && right)  return false;
        else if(left && !right) return false;
        else if(!left && !right)    return true;
        else if(left->val != right->val)    return false;
        else return (check(left->left, right->right) && check(left->right, right->left));
    }
    bool isSymmetric(TreeNode* root) {
        if(!root)   return true;
        return check(root->left, root->right);
   }
};

迭代

通过队列存储节点，同一层左右子树对应节点先后入队列。
时间复杂度O(n)，空间复杂度O(n)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root)   return true;
        queue<TreeNode*> nodes;
        nodes.push(root->left);
        nodes.push(root->right);
        while(nodes.size()>0) {
            int size = nodes.size()/2;
            for(int i=0; i<size; i++) {
                TreeNode *left = nodes.front(); nodes.pop();
                TreeNode *right = nodes.front(); nodes.pop();
                if((!left&&right) || (!right&&left))    return false;
                else {
                    if(right && left) {
                        if(left->val != right->val) return false;
                        nodes.push(left->left);
                        nodes.push(right->right);
                        nodes.push(left->right);
                        nodes.push(right->left);
                    }
                }
            }
        }
        return true;
   }
};