题目

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：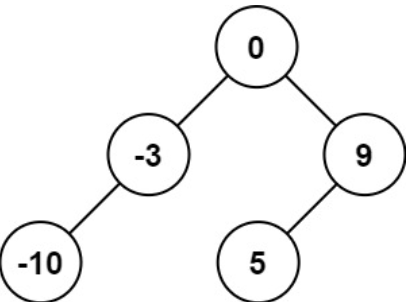
image.png

  1. 输入：nums = [-10,-3,0,5,9]
  2. 输出：[0,-3,9,-10,null,5]
  3. 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

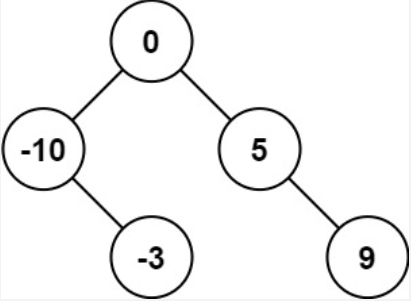
image.png
示例 2：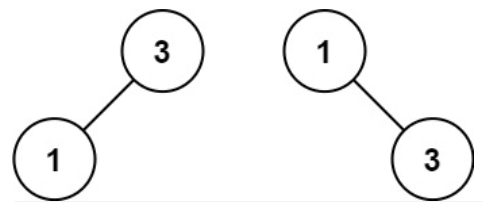
image.png

  1. 输入：nums = [1,3]
  2. 输出：[3,1]
  3. 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

  • 1 <= nums.length <= 10^4
  • -10^4 <= nums[i] <= 10^4

  • nums 按 严格递增 顺序排列

    解题方法

    递归

    由于数组严格有序，在数组中间构建节点，将数组分为左右两部分，再递归处理左右子树。
    时间复杂度O(n)，空间复杂度O(logn)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  TreeNode* getBST(vector<int>& nums, int left, int right) {
      if(left>right)  return NULL;
      if(left==right) return new TreeNode(nums[left]);
      int mid = left+(int)((right-left+1)/2);
      TreeNode* root = new TreeNode(nums[mid]);
      root->left = getBST(nums, left, mid-1);
      root->right = getBST(nums, mid+1, right);

      return root;
  }

  TreeNode* sortedArrayToBST(vector<int>& nums) {
      return getBST(nums, 0, nums.size()-1);
  }
};

    迭代

    通过队列模拟不断分割数组的过程。
    时间复杂度O(n)，空间复杂度O(logn)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  TreeNode* sortedArrayToBST(vector<int>& nums) {
      TreeNode* root = new TreeNode(0);
      queue<TreeNode*> nodes;
      queue<int> left;
      queue<int> right;
      nodes.push(root);
      left.push(0);
      right.push(nums.size()-1);
      while(nodes.size()) {
          TreeNode* cur = nodes.front();
          int l = left.front();
          int r = right.front();
          nodes.pop(); left.pop(); right.pop();
          int mid = (l+r+1)/2;
          cur->val = nums[mid];
          if(l<mid) {
              cur->left = new TreeNode(0);
              nodes.push(cur->left);
              left.push(l);
              right.push(mid-1);
          }
          if(r>mid) {
              cur->right = new TreeNode(0);
              nodes.push(cur->right);
              left.push(mid+1);
              right.push(r);
          }
      }

      return root;
  }
};