题目

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：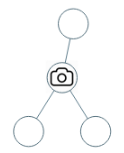
image.png

  1. 输入：[0,0,null,0,0]
  2. 输出：1
  3. 解释：如图所示，一台摄像头足以监控所有节点。

示例 2：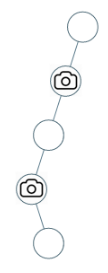
image.png

  1. 输入：[0,0,null,0,null,0,null,null,0]
  2. 输出：2
  3. 解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

  • 给定树的节点数的范围是 [1, 1000]。

  • 每个节点的值都是 0。

    解题方法

    贪心

    局部最优：一个相机覆盖面积最大化（在叶子结点的父节点上）。
    对于一个节点由三种状态，表述如下：

    • 0：该节点未被监控，需要被监控
    • 1：该节点被监控，不需要提供监控
    • 2：该节点有相机，可以为周围节点提供监控。

该题采用后序遍历的方式，首先遍历左右子树，再根据左右子树的情况判定当前节点是否需要提供摄像头，判定如下：

  • if(left==0 || right==0):当前节点需要提供摄像头给子节点。
  • else if(left==2 || right==2):当前节点可以被子节点的摄像头覆盖。
  • else:当前节点的左右子树均已被监控，需要当前节点的父节点提供监控

时间复杂度O(n)，空间复杂度O(n)
C++代码：

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13.     int sum = 0;
  14. public:
  15.     int dfs(TreeNode* cur) {
  16.         if(!cur) return 1;
  18.         int left = dfs(cur->left);
  19.         int right = dfs(cur->right);
  21.         if(left==0 || right==0) {
  22.             sum++;
  23.             return 2;
  24.         }
  25.         else if(left==2 || right==2)    return 1;
  26.         else    return 0;   
  27.     }
  28.     int minCameraCover(TreeNode* root) {
  29.         int cur = dfs(root);
  30.         if(cur==0) sum++;
  31.         return sum;
  32.     }
  33. };