题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

  
  示例 1：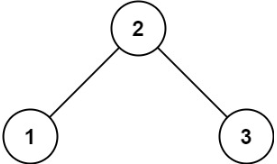
  

  输入：root = [2,1,3]
  输出：true

  示例 2：
  

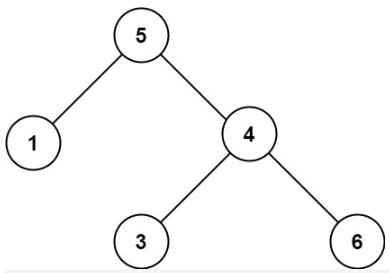
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

解题方法

递归

设定父节点的上下限，递归判断各自节点，同时缩小上下限。
时间复杂度O(n)，空间复杂度O(n)。
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool dfs(TreeNode* p, long long upper, long long lower) {
        if(!p)  return true;
        if(p->val<=lower || p->val>=upper)    return false;
        return dfs(p->left, p->val, lower) && dfs(p->right, upper, p->val);
    }
    bool isValidBST(TreeNode* root) {
        return dfs(root, LONG_MAX, LONG_MIN);
    }
};

中序遍历

对于搜索二叉树，其中序遍历为递增数列，因此只需要判断当前数是否大于前一个数即可。采用 Morris 遍历方法，节省空间（直接break;或return false;会报stack overflow的错误，应该是修改了二叉树的指针指向导致的）。
时间复杂度O(n)，空间复杂度O(1)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        TreeNode* mostright,* cur;
        cur = root;
        long long flag = LONG_MIN;
        bool result = true;
        while(cur!=NULL) {
            mostright = cur->left;
            if(mostright) {
                while(mostright->right && mostright->right!=cur)    mostright = mostright->right;
                if(!mostright->right) {
                    mostright->right = cur;
                    cur = cur->left;
                }
                else {
                    mostright->right = NULL;
                    if(cur->val <= flag)    result =  false;
                    flag = cur->val;
                    cur = cur->right;
                }
            }
            else {
                if(cur->val <= flag)    result =  false;   
                flag = cur->val;
                cur = cur->right;
            }           
        }
        return result;
    }
};