题目

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：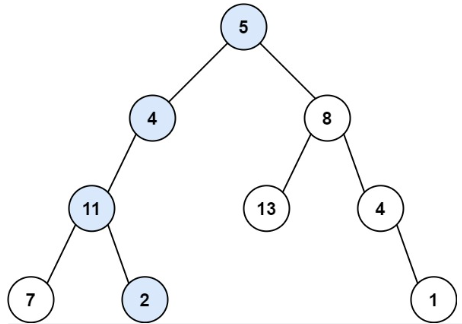
image.png

  1. 输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
  2. 输出：true
  3. 解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：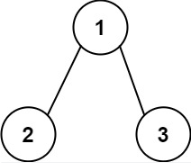
image.png

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

  • 树中节点的数目在范围 [0, 5000] 内
  • -1000 <= Node.val <= 1000

  • -1000 <= targetSum <= 1000

    解题方法

    递归 DFS

    通过 DFS 遍历所有路径，没经过一个节点便在计数值中减去当前节点数值，当碰到叶子节点时，若计数值与当前节点数值相等，则返回true；反之则返回false。
    时间复杂度O(n)，空间复杂度O(n)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  bool hasPathSum(TreeNode* root, int targetSum) {
      if(!root)     return false;
      if(!root->left && !root->right && targetSum==root->val)     return true;

      return hasPathSum(root->left, targetSum-root->val) || hasPathSum(root->right, targetSum-root->val);
  }
};

    迭代

    通过迭代层序遍历各节点，并记录各路径之和。
    时间复杂度O(n)，空间复杂度O(n)
    C++代码：

    /**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
  bool hasPathSum(TreeNode* root, int targetSum) {
      queue<TreeNode*> nodes;
      queue<int> vals;
      if(!root)   return false;
      nodes.push(root);
      vals.push(root->val);
      while(nodes.size()>0) {
          TreeNode* cur = nodes.front(); nodes.pop();
          int tmp = vals.front(); vals.pop();
          if(!cur->left && !cur->right && targetSum == tmp)       return true;
          if(cur->left) {
              nodes.push(cur->left);
              vals.push(tmp+cur->left->val);
          }
          if(cur->right) {
              nodes.push(cur->right);
              vals.push(tmp+cur->right->val);
          }
      }

      return false;
  }
};