题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；

如果找到了，删除它。

示例 1: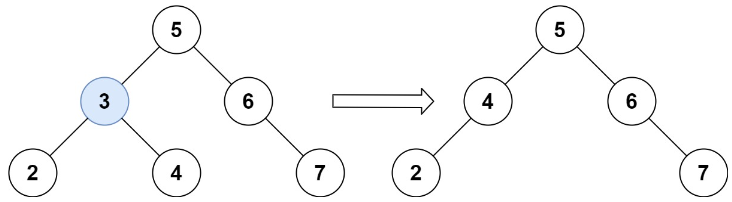

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

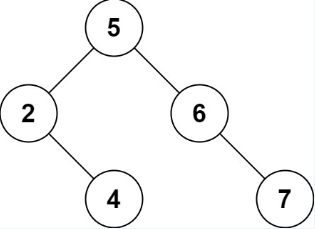
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

节点数的范围 [0, 10^4].
-10^5 <= Node.val <= 10^5
节点值唯一
root 是合法的二叉搜索树

-10^5 <= key <= 10^5

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

解题方法

递归+迭代（均衡）

采用递归与迭代结合的方法处理二叉搜索树中的子树，具体流程如下：

1. 深度优先在二叉搜索树中查找`key`**（迭代）**
1. 若未查找到`key`
   1. 返回`root`
3. 若查找到`key`对应节点`cur`
   1. 如果`cur`的左子树存在
      1. 遍历找到左子树的最右节点`mostright`**（迭代）**
      1. 用`mostright`值替换`cur`的值
      1. 递归调用该函数，在`cur`左子树中删除`mostright`节点。**（递归）**
   2. 如果`cur`的左子树不存在，但右子树存在
      1. 遍历找到右子树的最左节点`mostleft`**（迭代）**
      1. 用`mostleft`值替换`cur`的值
      1. 递归调用该函数，在`cur`右子树中删除`mostleft`节点。**（递归）**
   3. 如果`cur`为叶子节点
      1. 如果`cur`即根节点，返回`NULL`。
      1. 如果`cur`存在父节点，将父节点中指向`cur`的指针指向`NULL`
4. 返回根节点

时间复杂度O(n)，空间复杂度O(n)（平均O(1)）
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode* cur = root;
        TreeNode* pre = root;
        while(cur) {
            if(cur->val==key)   break;
            pre = cur;
            if(cur->val>key)    cur = cur->left;
            else    cur = cur->right;
        }
        if(!cur)    return root;
        if(cur->left) {
            TreeNode* mostright = cur->left;
            while(mostright->right) mostright = mostright->right;
            cur->val = mostright->val;
            cur->left = deleteNode(cur->left, cur->val);
        }
        else if(cur->right) {
            TreeNode* mostleft = cur->right;
            while(mostleft->left) mostleft = mostleft->left;
            cur->val = mostleft->val;
            cur->right = deleteNode(cur->right, cur->val);
        }
        else {
            if(cur==root)   return NULL;
            if(pre->left==cur)  pre->left = NULL;
            if(pre->right==cur) pre->right = NULL;
        }

        return root;
    }
};

递归

通过递归的方式处理子树。
时间复杂度O(n)，空间复杂度O(n)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(!root)   return NULL;
        if(root->val>key) {
            root->left = deleteNode(root->left, key);
            return root;
        }
        if(root->val<key) {
            root->right = deleteNode(root->right, key);
            return root;
        }   
        if(root->val==key) {
            if(!root->left && !root->right) return NULL;
            if(!root->left) return root->right;
            if(!root->right) return root->left;
            TreeNode* mostright = root->left;
            while(mostright->right) mostright = mostright->right;
            root->left = deleteNode(root->left, mostright->val);
            mostright->right = root->right;
            mostright->left = root->left;
            return mostright;
        }
        return root;
    }
};

迭代（空间复杂度最优）

通过迭代的方式完成遍历及删除，降低空间复杂度。
时间复杂度O(n)，空间复杂度O(1)
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode* cur = root;
        TreeNode* pre = NULL;
        while(cur) {
            if(cur->val==key)   break;
            pre = cur;
            if(cur->val>key)    cur = cur->left;
            else    cur = cur->right;
        }
        if(!cur)    return root;
        if(!cur->left && !cur->right)   cur = NULL;
        else if(!cur->left)  cur = cur->right;
        else if(!cur->right)  cur = cur->left;
        else {
            TreeNode* mostright = cur->left;
            TreeNode* sub_pre = cur;
            while(mostright->right) {
                sub_pre = mostright;
                mostright = mostright->right;
            }
            if(sub_pre==cur)    cur->left = mostright->left;
            else    sub_pre->right = mostright->left;
            mostright->right = cur->right;
            mostright->left = cur->left;
            cur = mostright;
        }
        if(!pre)    return cur;
        else {
            if(pre->left && pre->left->val==key)  pre->left = cur;
            else pre->right = cur;
        }
        return root;
    }
};

LeetCode

450. 删除二叉搜索树中的节点

题目

解题方法

递归+迭代（均衡）

递归

迭代（空间复杂度最优）