题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1: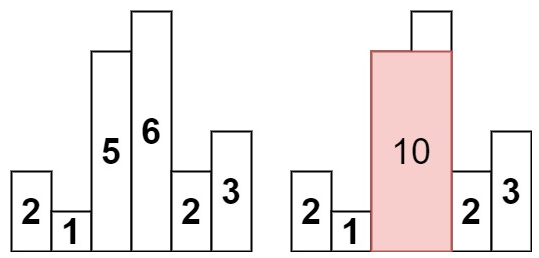
image.png

  1. 输入：heights = [2,1,5,6,2,3]
  2. 输出：10
  3. 解释：最大的矩形为图中红色区域，面积为 10

示例 2：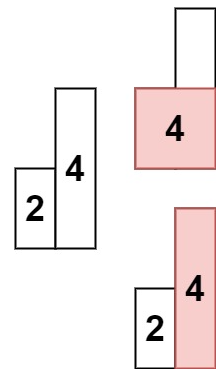
image.png

输入： heights = [2,4]
输出： 4

提示：

  • 1 <= heights.length <=10^5
  • 0 <= heights[i] <= 10^4

    解题方法

    单调栈

    本题相较于 42. 接雨水 区别在于，填充是向柱子内部进行的，因此决定因素是两侧的较小元素（即将入栈的较小元素和栈顶下一个较小元素）而不是最小元素。故本题需要采用降序单调栈，并且为了将两侧的元素也能考虑到，需要在开始和结尾添加0元素。
    时间复杂度O(n)，空间复杂度O(n)
    C++代码：
    class Solution {
public:
  int largestRectangleArea(vector<int>& heights) {
      int size = heights.size();
      heights.emplace(heights.end(), 0);
      heights.emplace(heights.begin(), 0);
      stack<int> st;
      int result = 0;
      for(int i=0; i<size+2; i++) {
          while(!st.empty() && heights[i] < heights[st.top()]) {
              int mid = heights[st.top()];
              st.pop();
              result = max(result, mid*(i-st.top()-1));
          }
          st.push(i);
      }
      return result;
  }
};